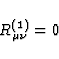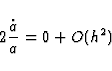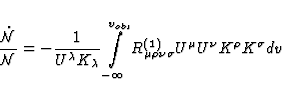

Next: Application to the scalar-tensor
Up: Scintillation in scalar-tensor theories
Previous: General theory of the
Now we assume the gravitational field to be very weak. So we put
| 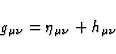 |
(49) |
where 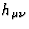 is a small perturbation of the flat spacetime
metric
is a small perturbation of the flat spacetime
metric 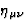 , and we systematically discard the
terms of order h2,h3,... in the following calculations. Thereafter, we
suppose that any quantity T (scalar or tensor) may be written as
, and we systematically discard the
terms of order h2,h3,... in the following calculations. Thereafter, we
suppose that any quantity T (scalar or tensor) may be written as
|
T = T(0) + T(1) + O(h2)
|
(50) |
where T(0) is the unperturbed quantity in flat spacetime and T(1)
denotes the perturbation of first-order with respect to 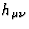 .
Henceforth, indices will be lowered with
.
Henceforth, indices will be lowered with 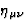 and
raised with
and
raised with 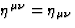 .
.
We shall put for the sake of simplicity
| 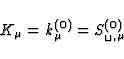 |
(51) |
Neglecting the first order terms in h, Eq.(12) gives
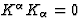 , whereas Eq.(17) reduces to the equation of a null
geodesic in flat spacetime related to Cartesian coordinates
, whereas Eq.(17) reduces to the equation of a null
geodesic in flat spacetime related to Cartesian coordinates
| 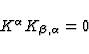 |
(52) |
In agreement with the assumptions made in Sect.3 to obtain Eqs.(29) and
(31), we
consider that at the zeroth order in 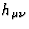 , the light emitted by the
source is described by a plane monochromatic wave in a flat spacetime. So we
suppose that the quantities
, the light emitted by the
source is described by a plane monochromatic wave in a flat spacetime. So we
suppose that the quantities 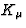 ,
, 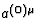 and consequently a(0)
are constants throughout the domain of propagation.
and consequently a(0)
are constants throughout the domain of propagation.
Moreover, we regard as negligible all the perturbations of gravitational
origin in the vicinity of the emitter (this hypothesis is natural for a source
at spatial infinity) and the quantity a0 in Eqs.(28) and (29) is given
consequently by
Furthermore, it results from 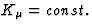 that
that 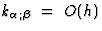 .
Therefore, terms like
.
Therefore, terms like 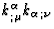 or
or
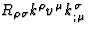 are of second order and
can be systematically disregarded.
are of second order and
can be systematically disregarded.
According to our general assumption in this section, the unit 4-velocity
of the observer may be expanded as
| 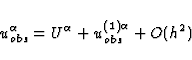 |
(54) |
at any point of 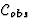 , with the definition
, with the definition
| 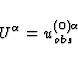 |
(55) |
It follows from (48) and from 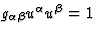 that
that
| 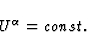 |
(56) |
and
| 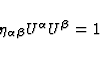 |
(57) |
From these last equations, we recover the fact that the unperturbed motion
of a freely falling observer is a time-like straight line in Minkowski
space-time.
Now we have to know the quantities 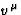 occurring in Eqs.(47) and (52)
at the lowest order. An elementary calculation shows that, in
Eqs.(46), the covariant differentiation may be replaced by the ordinary
differentiation. So we have to solve the system
occurring in Eqs.(47) and (52)
at the lowest order. An elementary calculation shows that, in
Eqs.(46), the covariant differentiation may be replaced by the ordinary
differentiation. So we have to solve the system
| 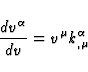 |
(58) |
together with the boundary conditions (34).
Assuming the expansion
| 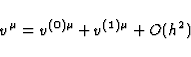 |
(59) |
it is easily seen that the unique solution of (62) and (34) is such that at any
point of the light ray 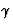 , the components
, the components 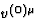 are constants
given by
are constants
given by
| 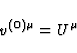 |
(60) |
Neglecting all the second order terms in (47) and (52), we finally obtain
and
| 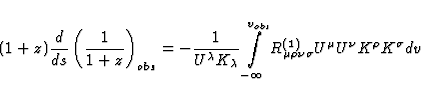 |
(61) |
all the integrations being performed along the unperturbed path of light.
In Eq.(66) 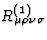 denotes the linearized curvature
tensor of the metric
denotes the linearized curvature
tensor of the metric 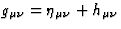 , i.e.
, i.e.
| 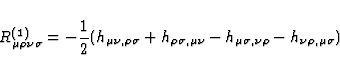 |
(62) |
and 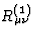 is the corresponding linearized Ricci tensor
is the corresponding linearized Ricci tensor
| 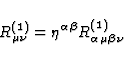 |
(63) |
It is worthy to note that the components 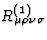 and
and 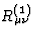 are gauge-invariant quantities. Indeed, under an
arbitrary infinitesimal coordinate transformation
are gauge-invariant quantities. Indeed, under an
arbitrary infinitesimal coordinate transformation 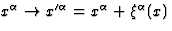 ,
, 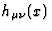 transforms into
transforms into
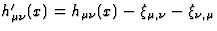 , and it is easily checked from (67) and (68) that
, and it is easily checked from (67) and (68) that
| 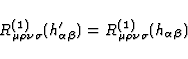 |
(64) |
| 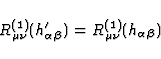 |
(65) |
This feature ensures that the right-hand sides of Eqs. (65) and (66) are
gauge-invariant quantities.
Equation (65) reveals that the first order geometrical scintillation
effect depends upon the gravitational field through the Ricci tensor only.
On the other side, it follows from (66) that the part of the scintillation due
to the spectral shift depends upon the curvature tensor.
These properties have remarkable consequences in general relativity.
Suppose that the light ray 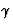 travels
in regions entirely free of matter. Since the linearized Einstein equations are
in a vacuum
travels
in regions entirely free of matter. Since the linearized Einstein equations are
in a vacuum
| 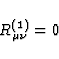 |
(66) |
it follows from Eq.(65) that
| 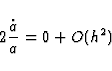 |
(67) |
As a consequence, 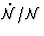 reduces to the contribution of
the change in the spectral shift
reduces to the contribution of
the change in the spectral shift
| 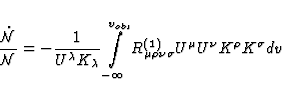 |
(68) |
From (72), we recover the conclusion previously drawn by Zipoy (1966) and
Zipoy & Bertotti (1968): within general relativity, gravitational waves
produce no first order geometrical scintillation.


Next: Application to the scalar-tensor
Up: Scintillation in scalar-tensor theories
Previous: General theory of the
10/9/1998
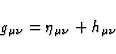
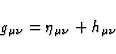
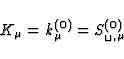
![]() , whereas Eq.(17) reduces to the equation of a null
geodesic in flat spacetime related to Cartesian coordinates
, whereas Eq.(17) reduces to the equation of a null
geodesic in flat spacetime related to Cartesian coordinates
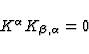
![]() , the light emitted by the
source is described by a plane monochromatic wave in a flat spacetime. So we
suppose that the quantities
, the light emitted by the
source is described by a plane monochromatic wave in a flat spacetime. So we
suppose that the quantities ![]() ,
, ![]() and consequently a(0)
are constants throughout the domain of propagation.
and consequently a(0)
are constants throughout the domain of propagation.
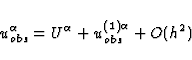
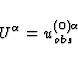
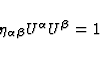
![]() occurring in Eqs.(47) and (52)
at the lowest order. An elementary calculation shows that, in
Eqs.(46), the covariant differentiation may be replaced by the ordinary
differentiation. So we have to solve the system
occurring in Eqs.(47) and (52)
at the lowest order. An elementary calculation shows that, in
Eqs.(46), the covariant differentiation may be replaced by the ordinary
differentiation. So we have to solve the system
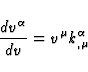
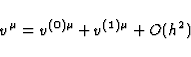
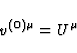
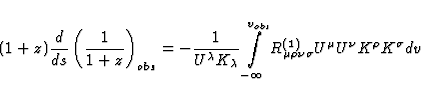
![]() denotes the linearized curvature
tensor of the metric
denotes the linearized curvature
tensor of the metric ![]() , i.e.
, i.e.
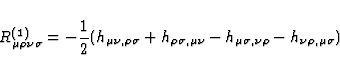
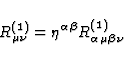
![]() and
and ![]() are gauge-invariant quantities. Indeed, under an
arbitrary infinitesimal coordinate transformation
are gauge-invariant quantities. Indeed, under an
arbitrary infinitesimal coordinate transformation ![]() ,
, ![]() transforms into
transforms into
![]() , and it is easily checked from (67) and (68) that
, and it is easily checked from (67) and (68) that
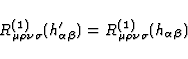
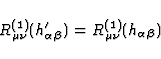
![]() travels
in regions entirely free of matter. Since the linearized Einstein equations are
in a vacuum
travels
in regions entirely free of matter. Since the linearized Einstein equations are
in a vacuum