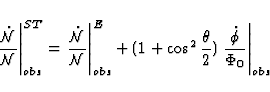

Next: Are observational tests possible?
Up: Scintillation in scalar-tensor theories
Previous: Weak-field approximation
The general theory developed in the above sections is valid for any metric
theory of gravity. Let us now examine the implications of Eqs.(65) and (66)
within the scalar-tensor theories of gravity.
The class of theories that we consider here is described by the action
![[*]](foot_motif.gif)
where R is the Ricci scalar curvature (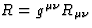 ),
), 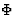 is
the scalar gravitational field, g is the determinant of the metric components
is
the scalar gravitational field, g is the determinant of the metric components
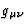 ,
, 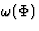 is an arbitrary function of the scalar field
is an arbitrary function of the scalar field 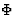 , and
, and
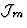 is the matter action. We assume that
is the matter action. We assume that 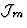 is a
functional of the metric and of the matter fields
is a
functional of the metric and of the matter fields 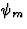 only. This means
that
only. This means
that 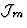 does not depend explicitly upon the scalar field
does not depend explicitly upon the scalar field 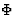 (it is the assumption of universal coupling between matter and metric).
(it is the assumption of universal coupling between matter and metric).
We consider here the weak-field approximation only. So we assume that the
scalar field 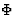 is of the form
is of the form
| 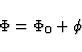 |
(69) |
where 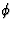 is a first order perturbation of an averaged constant value
is a first order perturbation of an averaged constant value
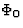 . Consequently, the field equations deduced from
(74) reduce to the following system:
. Consequently, the field equations deduced from
(74) reduce to the following system:
| 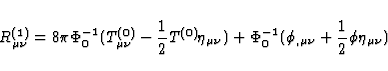 |
(70) |
| 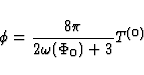 |
(71) |
where 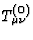 is the energy-momentum tensor of the matter fields
is the energy-momentum tensor of the matter fields
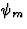 at the lowest order,
at the lowest order, 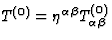 and
and 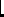 denotes the
d'Alembertian operator on Minkowski spacetime:
denotes the
d'Alembertian operator on Minkowski spacetime: 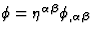 .
.
It is easily seen that any solution 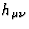 to the field equations
(76) is given by
to the field equations
(76) is given by ![[*]](foot_motif.gif)
| 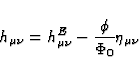 |
(72) |
where 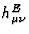 is a solution to the equations
is a solution to the equations
| 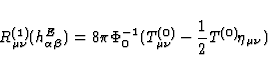 |
(73) |
which are simply the linearized Einstein equations with an effective
gravitational constant 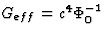 . Indeed, inserting (78) in
(67) yields the following expression for the curvature tensor
. Indeed, inserting (78) in
(67) yields the following expression for the curvature tensor
from which one deduces the Ricci tensor
| 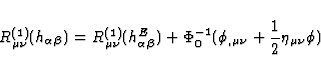 |
(74) |
Then substituting for 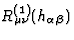 from its expression
(81) into the field equations (76) gives Eqs.(79), thus proving the proposition.
from its expression
(81) into the field equations (76) gives Eqs.(79), thus proving the proposition.
The decomposition (78) of the gravitational perturbation 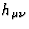 implies that each term contributing to
implies that each term contributing to 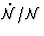 can be split
into a part built from the Einsteinian perturbation
can be split
into a part built from the Einsteinian perturbation 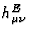 only
and into an other part built from the scalar field
only
and into an other part built from the scalar field 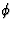 alone. In what
follows, we use the superscript ST for a functional of a solution
alone. In what
follows, we use the superscript ST for a functional of a solution 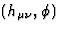 to the field equations (76)-(77) and the superscript E for the same
kind of functional evaluated only with the corresponding solution
to the field equations (76)-(77) and the superscript E for the same
kind of functional evaluated only with the corresponding solution 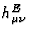 .
.
In order to perform the calculation of the integrals (65) and (66), we note
that 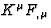 is the usual total derivative of the quantity F along
the unperturbed ray path, which implies that
is the usual total derivative of the quantity F along
the unperturbed ray path, which implies that
| 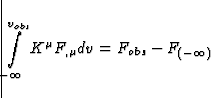 |
(75) |
The 4-vector 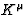 (supposed here to be future oriented, i.e
such that K0 > 0) gives the direction of propagation of the light coming from
the observed source. For a given observer moving with the 4-velocity
(supposed here to be future oriented, i.e
such that K0 > 0) gives the direction of propagation of the light coming from
the observed source. For a given observer moving with the 4-velocity 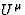 ,
let us put
,
let us put
| 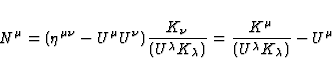 |
(76) |
We have 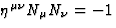 . Since
. Since 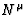 is orthogonal to
is orthogonal to
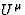 by construction,
by construction, 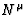 can be identified to the unit 3-vector
can be identified to the unit 3-vector
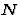 giving the direction of propagation of the light ray in the usual
3-space of the observer.
giving the direction of propagation of the light ray in the usual
3-space of the observer.
Using (76), (77), (80) and the assumption 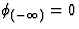 , it is
easily seen that (65) and (66) can be respectively written as
, it is
easily seen that (65) and (66) can be respectively written as
| 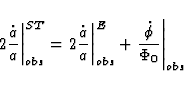 |
(77) |
and
where
| 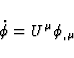 |
(78) |
and
| 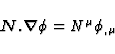 |
(79) |
As a consequence, the rate of variation in the photon flux as received by
the observer is given by the general formula
| 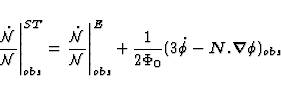 |
(80) |
In a vacuum 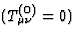 , the metric
, the metric 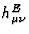 satisfies the linearized Einstein field equations (71) and Eq.(84) reduces to
satisfies the linearized Einstein field equations (71) and Eq.(84) reduces to
| 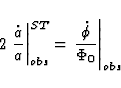 |
(81) |
In Eq.(88), 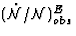 is reduced to the term
given by Eq.(73), where
is reduced to the term
given by Eq.(73), where 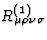 is constructed with
is constructed with
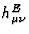 .
.
It follows from (89) that contrary to general relativity, the scalar-tensor
theories (defined by (74)) predict the existence of a first-order geometrical
scintillation effect produced by gravitational waves. This effect is
proportional to the amplitude of the scalar perturbation. It should be noted
that an effect of the same order of magnitude is also due to the change in the
spectral shift.
To finish, let us briefly examine the case where the scalar wave 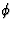 is
locally plane (it is a reasonable assumption if the source of gravitational
wave is far from the observer). Thus we can put in the vicinity of the observer
located at the point xobs
is
locally plane (it is a reasonable assumption if the source of gravitational
wave is far from the observer). Thus we can put in the vicinity of the observer
located at the point xobs
| 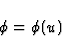 |
(82) |
where u is a phase function which admits the expansion
| 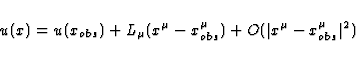 |
(83) |
with
| 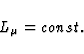 |
(84) |
It follows from Eq.(77) with T(0) = 0 that 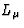 is a null vector
of Minkowski spacetime.
is a null vector
of Minkowski spacetime.
Replacing 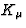 by
by 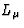 in (83) defines the
spacelike vector
in (83) defines the
spacelike vector 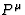 , which can be identified with the unit 3-vector
, which can be identified with the unit 3-vector
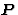 giving the direction of propagation of the scalar wave in the
3-space of the observer. Then introducing the angle
giving the direction of propagation of the scalar wave in the
3-space of the observer. Then introducing the angle 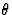 between
between
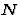 and
and 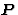 , a simple calculation yields
, a simple calculation yields
| 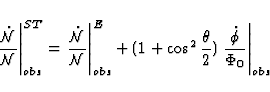 |
(85) |
This formula shows that the contribution of the scalar wave to the
scintillation cannot be zero, whatever be the direction of observation of the
distant light source.


Next: Are observational tests possible?
Up: Scintillation in scalar-tensor theories
Previous: Weak-field approximation
10/9/1998
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)
![]() is of the form
is of the form
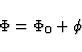
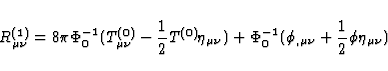
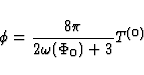
![]() to the field equations
(76) is given by
to the field equations
(76) is given by ![[*]](foot_motif.gif)
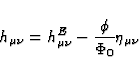
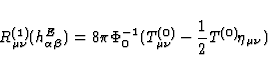
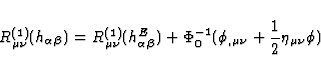
![]() implies that each term contributing to
implies that each term contributing to ![]() can be split
into a part built from the Einsteinian perturbation
can be split
into a part built from the Einsteinian perturbation ![]() only
and into an other part built from the scalar field
only
and into an other part built from the scalar field ![]() alone. In what
follows, we use the superscript ST for a functional of a solution
alone. In what
follows, we use the superscript ST for a functional of a solution ![]() to the field equations (76)-(77) and the superscript E for the same
kind of functional evaluated only with the corresponding solution
to the field equations (76)-(77) and the superscript E for the same
kind of functional evaluated only with the corresponding solution ![]() .
.![]() is the usual total derivative of the quantity F along
the unperturbed ray path, which implies that
is the usual total derivative of the quantity F along
the unperturbed ray path, which implies that
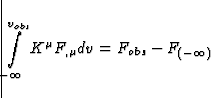
![]() (supposed here to be future oriented, i.e
such that K0 > 0) gives the direction of propagation of the light coming from
the observed source. For a given observer moving with the 4-velocity
(supposed here to be future oriented, i.e
such that K0 > 0) gives the direction of propagation of the light coming from
the observed source. For a given observer moving with the 4-velocity ![]() ,
let us put
,
let us put
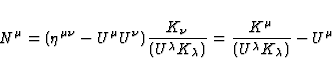
![]() , it is
easily seen that (65) and (66) can be respectively written as
, it is
easily seen that (65) and (66) can be respectively written as
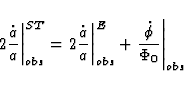
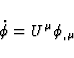
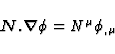
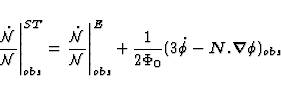
![]() , the metric
, the metric ![]() satisfies the linearized Einstein field equations (71) and Eq.(84) reduces to
satisfies the linearized Einstein field equations (71) and Eq.(84) reduces to
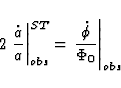
![]() is reduced to the term
given by Eq.(73), where
is reduced to the term
given by Eq.(73), where ![]() is constructed with
is constructed with
![]() .
.![]() is
locally plane (it is a reasonable assumption if the source of gravitational
wave is far from the observer). Thus we can put in the vicinity of the observer
located at the point xobs
is
locally plane (it is a reasonable assumption if the source of gravitational
wave is far from the observer). Thus we can put in the vicinity of the observer
located at the point xobs
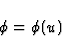
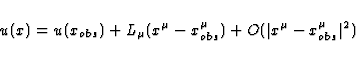
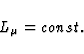
![]() is a null vector
of Minkowski spacetime.
is a null vector
of Minkowski spacetime.
![]() by
by ![]() in (83) defines the
spacelike vector
in (83) defines the
spacelike vector ![]() , which can be identified with the unit 3-vector
, which can be identified with the unit 3-vector
![]() giving the direction of propagation of the scalar wave in the
3-space of the observer. Then introducing the angle
giving the direction of propagation of the scalar wave in the
3-space of the observer. Then introducing the angle ![]() between
between
![]() and
and ![]() , a simple calculation yields
, a simple calculation yields