

Next: Weak-field approximation
Up: Scintillation in scalar-tensor theories
Previous: Notations and definitions
In a region of spacetime free of electric charge, the propagation equations for
the electromagnetic vector potential 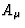 are (e.g., Misner et
al. 1973)
are (e.g., Misner et
al. 1973)
| 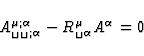 |
(3) |
when 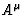 is chosen to obey the Lorentz gauge condition
is chosen to obey the Lorentz gauge condition
| 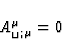 |
(4) |
It is convenient here to treat 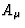 as a complex vector.
Hence the electromagnetic field tensor
as a complex vector.
Hence the electromagnetic field tensor 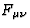 is given by
is given by
| 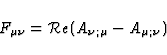 |
(5) |
The corresponding electromagnetic energy-momentum tensor is defined by
| ![\begin{displaymath}
T^{\mu \nu} = \frac{1}{4 \pi} \left[-F^{\mu \rho} F^{\nu}_{....
...rac{1}{4} F^{\alpha \beta} F_{\alpha \beta} g^{\mu \nu} \right]\end{displaymath}](img19.gif) |
(6) |
where 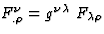 . The components of
this tensor satisfy the conservation equations
. The components of
this tensor satisfy the conservation equations
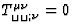 as a consequence of Eqs.(3).
as a consequence of Eqs.(3).
For an observer located at the spacetime point x and moving with the
unit 4-velocity 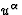 , the density of electromagnetic energy flux is
given by the Poynting vector
, the density of electromagnetic energy flux is
given by the Poynting vector
| 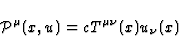 |
(7) |
and the density of electromagnetic energy as measured by the observer is
| 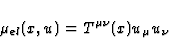 |
(8) |
In this paper, we use the geometrical optics approximation. So we assume
that there exist wave solutions to Eqs.(3) which admit a development of the form
| ![\begin{displaymath}
A^{\mu}(x,\xi) = [a^{\mu}(x) + O(\xi)] \exp(\frac{i}{\xi} \hat{S}(x))\end{displaymath}](img25.gif) |
(9) |
where 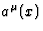 is a slowly varying complex vector amplitude,
is a slowly varying complex vector amplitude, 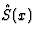 is a real function and
is a real function and 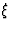 a dimensionless parameter which tends to zero as
the typical wavelength of the wave becomes shorter and shorter. A solution like
(9) represents a quasi plane, locally monochromatic wave of high frequency
(Misner et al. 1973).
a dimensionless parameter which tends to zero as
the typical wavelength of the wave becomes shorter and shorter. A solution like
(9) represents a quasi plane, locally monochromatic wave of high frequency
(Misner et al. 1973).
Let us define the phase S and the vector field 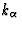 by the
relations
by the
relations
| 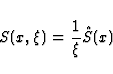 |
(10) |
and
| 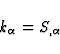 |
(11) |
Inserting (9) into Eqs.(3) and (4), then retaining only the leading terms of
order 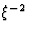 and
and 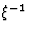 , yield the fundamental
equations of geometrical optics
, yield the fundamental
equations of geometrical optics
| 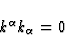 |
(12) |
| 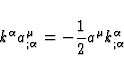 |
(13) |
with the gauge condition
| 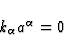 |
(14) |
Light rays are defined to be the curves whose tangent vector field is
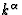 . So the parametric equations
. So the parametric equations 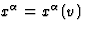 of the
light rays are solutions to the differential equations
of the
light rays are solutions to the differential equations
| 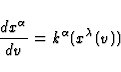 |
(15) |
where v is an affine parameter. Differentiating Eq.(12) and noting that
| 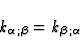 |
(16) |
follows from (11), it is easily seen that 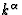 satisfies the
propagation equations
satisfies the
propagation equations
| 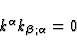 |
(17) |
These equations, together with (12), show that the light rays are null
geodesics.
Inserting (9) into (5) and (6) gives the approximate expression for
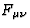
| ![\begin{displaymath}
F_{\mu \nu} = {\cal{R}}e[i(k_{\mu} a_{\nu} - k_{\nu} a_{\mu}) e^{iS}] \end{displaymath}](img42.gif) |
(18) |
and for 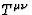 averaged over a period
averaged over a period
| 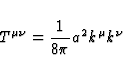 |
(19) |
where a is the scalar amplitude defined by
![[*]](foot_motif.gif)
| 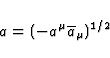 |
(20) |
From (7) and (19), it is easily seen that the Poynting vector is
proportional to the null tangent vector 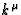 .This means that the energy of the wave is transported
along each ray with the speed of light. Let us denote by
.This means that the energy of the wave is transported
along each ray with the speed of light. Let us denote by 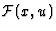 the
energy flux received by an observer located at x and moving with the
4-velocity
the
energy flux received by an observer located at x and moving with the
4-velocity 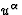 : by definition,
: by definition, 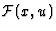 is the amount of
radiating energy flowing per unit proper time across a unit surface orthogonal
to the direction of propagation. It follows from (8) and (19) that
is the amount of
radiating energy flowing per unit proper time across a unit surface orthogonal
to the direction of propagation. It follows from (8) and (19) that
| 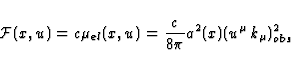 |
(21) |
This formula enables us to determine the photon flux 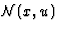 received by the observer located at x and moving with the 4-velocity
received by the observer located at x and moving with the 4-velocity
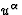 . Since the 4-momentum of a
photon is
. Since the 4-momentum of a
photon is 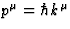 , the energy of the photon as measured by the
observer is
, the energy of the photon as measured by the
observer is 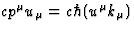 . We have therefore
. We have therefore
| 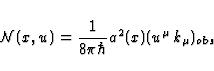 |
(22) |
The spectral shift z of a light source (emitter) as measured by an observer
is given by (e.g. G.F.R. Ellis, 1971)
| 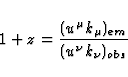 |
(23) |
Consequently, the photon flux 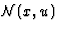 may be written as
may be written as
| 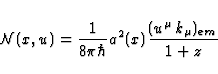 |
(24) |
The scalar amplitude a can be written in the form of an integral along
the light ray  joining the source to the observer located at x.
Multiplying Eq.(13) by
joining the source to the observer located at x.
Multiplying Eq.(13) by 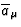 yields the propagation equation
for a
yields the propagation equation
for a
| 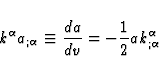 |
(25) |
where d/dv denotes the total differentiation of a scalar function along
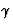 . Then, integrating (25) gives
. Then, integrating (25) gives
| 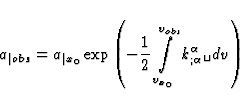 |
(26) |
where x0 is an arbitrary point on the light ray 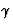 .
.
In the following, we consider that the light source is at spatial
infinity. We suppose the existence of coordinate systems 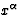 such
that on any
hypersurface x0 = const.,
such
that on any
hypersurface x0 = const., 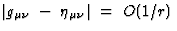 when
when
![$r~=~[\sum_{i=1}^3~(x^i)^2]^{1/2}~\rightarrow~\infty$](img62.gif) , with
, with
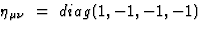 .
We require that in such coordinate systems the quantities
.
We require that in such coordinate systems the quantities 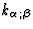 ,
,
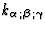 and
and 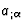 respectively fulfill the
asymptotic conditions
respectively fulfill the
asymptotic conditions
| 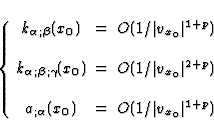 |
(27) |
when 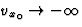 , with p > 0.
Moreover, we assume that the scalar amplitude
a|x0 in Eq.(26) remains bounded when
, with p > 0.
Moreover, we assume that the scalar amplitude
a|x0 in Eq.(26) remains bounded when 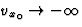 and
we put
and
we put
| 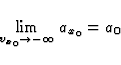 |
(28) |
It results from these assumptions that a|obs may be written as
| 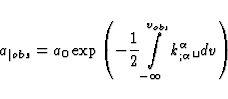 |
(29) |
Now, let us differentiate 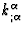 with respect to v
along
with respect to v
along 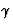 . Applying (1) and (2), then taking (16) and (17) into
account, we obtain the relation (Sachs 1961)
. Applying (1) and (2), then taking (16) and (17) into
account, we obtain the relation (Sachs 1961)
| 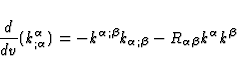 |
(30) |
As a consequence, we can write
| ![\begin{displaymath}
\int \limits_{-\infty}^{v_{obs}} k^{\alpha}_{; \alpha} \verb...
... k^{\alpha} k^{\beta} +
k^{\alpha;\beta} k_{\alpha;\beta}] dv' \end{displaymath}](img73.gif) |
(31) |
The convergence of the integrals is ensured by conditions (27).
Equations (29) and (31) allow to determine the factor a2(x) in
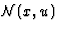 from the energy content of the regions crossed by the light
rays and from the geometry of the rays themselves.
from the energy content of the regions crossed by the light
rays and from the geometry of the rays themselves.
It is well known that 1/(1+z) (or (1+z)) can also be obtained in the
form of an integral along the light ray 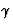 (see e.g. Ellis 1971 or
Schneider et al. 1992). However, the corresponding formula will not be
useful for our discussion and we will not develop it here.
(see e.g. Ellis 1971 or
Schneider et al. 1992). However, the corresponding formula will not be
useful for our discussion and we will not develop it here.
In fact, the scintillation phenomenon consists in a variation of
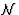 with respect to time. For this reason, it is more convenient to
calculate the total derivative of
with respect to time. For this reason, it is more convenient to
calculate the total derivative of 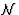 along the world-line
along the world-line
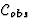 of a given observer, moving at the point x with the
4-velocity
of a given observer, moving at the point x with the
4-velocity 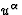 .
.
Given a scalar or tensorial quantity F, we denote by 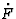 the total
covariant differentiation along
the total
covariant differentiation along 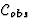 defined by
defined by
| 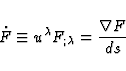 |
(32) |
where 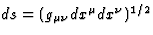 is the line element between
two events
is the line element between
two events 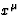 and
and 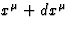 on
on 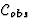 .
.
In Eq.(24), the quantity 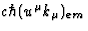 is the energy of a photon
emitted by an
atom of the light source as measured by an observer comoving with this atom. So
is the energy of a photon
emitted by an
atom of the light source as measured by an observer comoving with this atom. So
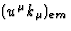 is a constant which depends only on the nature of
the atom (this constant characterizes the emitted spectral line). Consequently,
the change in the photon flux with respect to time is simply due to the change
in the scalar amplitude a and to the change in the spectral shift z.
From (24), we obtain at each point x of
is a constant which depends only on the nature of
the atom (this constant characterizes the emitted spectral line). Consequently,
the change in the photon flux with respect to time is simply due to the change
in the scalar amplitude a and to the change in the spectral shift z.
From (24), we obtain at each point x of 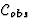
| 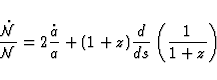 |
(33) |
Henceforth, we shall call the contribution 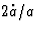 in Eq.(33) the
geometrical scintillation because the variations in a are related to the
focusing properties of light rays by gravitational fields
(see G.F.R.Ellis 1971 and references therein; see also Misner et al.
1973).
in Eq.(33) the
geometrical scintillation because the variations in a are related to the
focusing properties of light rays by gravitational fields
(see G.F.R.Ellis 1971 and references therein; see also Misner et al.
1973).
Let us now try to find expressions for 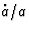 and
and 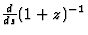 in the
form of integrals along
in the
form of integrals along 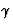 . In what follows, we assume that the ray
. In what follows, we assume that the ray
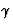 hits at each of its points x(v) a vector field
hits at each of its points x(v) a vector field 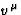 which
satisfies the boundary condition
which
satisfies the boundary condition
| 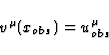 |
(34) |
Let us emphasize that 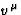 can be chosen arbitrarily at any point x
which does not belong to the world line
can be chosen arbitrarily at any point x
which does not belong to the world line 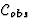 (for example,
(for example,
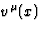 could be the unit 4-velocity of an observer at x, an
assumption which is currently made in cosmology; however we shall make a more
convenient choice for
could be the unit 4-velocity of an observer at x, an
assumption which is currently made in cosmology; however we shall make a more
convenient choice for 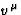 in what follows).
in what follows).
It results from the boundary conditions (27) and (34) that 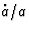 may
be written as
may
be written as
| ![\begin{displaymath}
\left.\frac{\dot{a}}{a}\right\vert _{obs} = \int \limits_{-\infty}^{v_{obs}} \frac{d}{dv}
[v^{\mu}(\ln a)_{;\mu}] dv\end{displaymath}](img90.gif) |
(35) |
Thus we have to transform the expression
| ![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = k^{\alpha}( v^{\mu}
(\ln a)_{;\mu})_{;\alpha}\end{displaymath}](img91.gif) |
(36) |
taken along 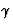 . Of course, we must take into account the propagation
equation (25) which could be rewritten as
. Of course, we must take into account the propagation
equation (25) which could be rewritten as
| 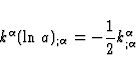 |
(37) |
Noting that
| 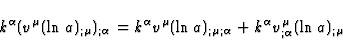 |
(38) |
then using the relation
| 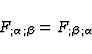 |
(39) |
which holds for any scalar F, we find
| ![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = v^{\mu} [k^{\alpha} (\ln
a)_{;\alpha}]_{;\mu} + [k,v]^{\mu} (\ln a)_{;\mu} \end{displaymath}](img95.gif) |
(40) |
where the bracket [k,v] of 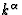 and
and 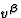 is the vector defined
by
is the vector defined
by
| ![\begin{displaymath}[k,v]
^{\mu} \equiv k^{\alpha} v^{\mu}_{;\alpha} - v^{\alpha} k^{\mu}_{;\alpha}\end{displaymath}](img97.gif) |
(41) |
Taking (37) into account, it is easily seen that
| ![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = -\frac{1}{2} v^{\mu}
k^{\alpha}_{;\alpha ;\mu} + [k,v]^{\mu} (\ln a)_{;\mu} \end{displaymath}](img98.gif) |
(42) |
Now, using the identity (1) and the definition (2) yields
| ![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = \frac{1}{2} R_{\mu \n...
... v^{\mu} k^{\alpha}_{;\mu ;\alpha} +[k,v]^{\mu} (\ln a)_{;\mu} \end{displaymath}](img99.gif) |
(43) |
Let us try to write the term
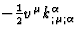 in the form of an integral
along
in the form of an integral
along 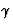 . In agreement with (27), we have at any point
x(v) of
. In agreement with (27), we have at any point
x(v) of 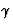 :
:
| 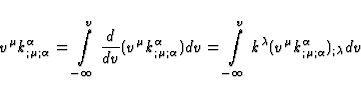 |
(44) |
A tedious but straightforward calculation using (1), (2) and (17) leads
to the following result
In the above formulae 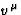 is an arbitrary vector. So we can
choose
is an arbitrary vector. So we can
choose 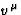 so that the transport equations
so that the transport equations
![[*]](foot_motif.gif)
| ![\begin{displaymath}[k,v]
^{\mu} = 0\end{displaymath}](img105.gif) |
(45) |
are satisfied along the ray 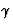 . Since (46) is a system of first order
partial differential equations in
. Since (46) is a system of first order
partial differential equations in 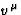 , there exists one and only one
solution satisfying the boundary conditions (34). With this choice,
, there exists one and only one
solution satisfying the boundary conditions (34). With this choice, 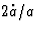 is given by the integral formula:
is given by the integral formula:
Now we look for an integral form for the total derivative 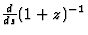 along
along 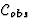 .
Henceforth, we suppose for the sake of simplicity that
the observer is freely falling, i.e. that
.
Henceforth, we suppose for the sake of simplicity that
the observer is freely falling, i.e. that 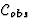 is a timelike
geodesic. So we have
is a timelike
geodesic. So we have
| 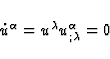 |
(46) |
Since 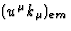 is a constant characterizing the observed
spectral line (see above), it follows from (23) and (48) that
is a constant characterizing the observed
spectral line (see above), it follows from (23) and (48) that
| 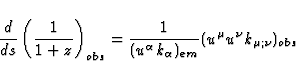 |
(47) |
Given an arbitrary vector field 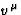 fulfilling the boundary
condition (34), Eq.(49) may be written as
fulfilling the boundary
condition (34), Eq.(49) may be written as
| 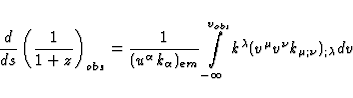 |
(48) |
Using (1), (17) and (41), a straightforward calculation gives the general
formula
which holds for any freely falling observer.
Now let us choose for 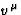 the vector field defined by (46) and (34).
We obtain
the vector field defined by (46) and (34).
We obtain


Next: Weak-field approximation
Up: Scintillation in scalar-tensor theories
Previous: Notations and definitions
10/9/1998
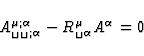
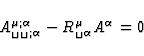
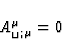
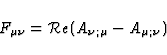
![\begin{displaymath}
T^{\mu \nu} = \frac{1}{4 \pi} \left[-F^{\mu \rho} F^{\nu}_{....
...rac{1}{4} F^{\alpha \beta} F_{\alpha \beta} g^{\mu \nu} \right]\end{displaymath}](img19.gif)
![]() , the density of electromagnetic energy flux is
given by the Poynting vector
, the density of electromagnetic energy flux is
given by the Poynting vector
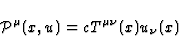
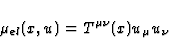
![\begin{displaymath}
A^{\mu}(x,\xi) = [a^{\mu}(x) + O(\xi)] \exp(\frac{i}{\xi} \hat{S}(x))\end{displaymath}](img25.gif)
![]() by the
relations
by the
relations
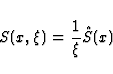
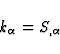
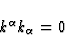
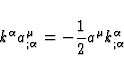
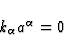
![]() . So the parametric equations
. So the parametric equations ![]() of the
light rays are solutions to the differential equations
of the
light rays are solutions to the differential equations
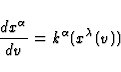
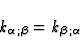
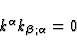
![]()
![\begin{displaymath}
F_{\mu \nu} = {\cal{R}}e[i(k_{\mu} a_{\nu} - k_{\nu} a_{\mu}) e^{iS}] \end{displaymath}](img42.gif)
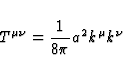
![[*]](foot_motif.gif)
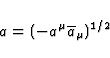
![]() .This means that the energy of the wave is transported
along each ray with the speed of light. Let us denote by
.This means that the energy of the wave is transported
along each ray with the speed of light. Let us denote by ![]() the
energy flux received by an observer located at x and moving with the
4-velocity
the
energy flux received by an observer located at x and moving with the
4-velocity ![]() : by definition,
: by definition, ![]() is the amount of
radiating energy flowing per unit proper time across a unit surface orthogonal
to the direction of propagation. It follows from (8) and (19) that
is the amount of
radiating energy flowing per unit proper time across a unit surface orthogonal
to the direction of propagation. It follows from (8) and (19) that
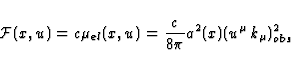
![]() received by the observer located at x and moving with the 4-velocity
received by the observer located at x and moving with the 4-velocity
![]() . Since the 4-momentum of a
photon is
. Since the 4-momentum of a
photon is ![]() , the energy of the photon as measured by the
observer is
, the energy of the photon as measured by the
observer is ![]() . We have therefore
. We have therefore
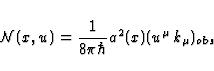
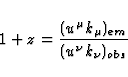
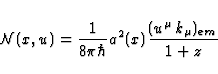
![]() joining the source to the observer located at x.
Multiplying Eq.(13) by
joining the source to the observer located at x.
Multiplying Eq.(13) by ![]() yields the propagation equation
for a
yields the propagation equation
for a
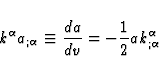
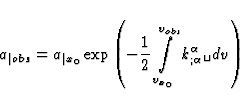
![]() such
that on any
hypersurface x0 = const.,
such
that on any
hypersurface x0 = const., ![]() when
when
![]() , with
, with
![]() .
We require that in such coordinate systems the quantities
.
We require that in such coordinate systems the quantities ![]() ,
,
![]() and
and ![]() respectively fulfill the
asymptotic conditions
respectively fulfill the
asymptotic conditions
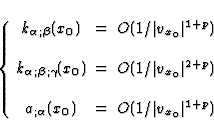
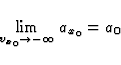
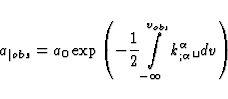
![]() with respect to v
along
with respect to v
along ![]() . Applying (1) and (2), then taking (16) and (17) into
account, we obtain the relation (Sachs 1961)
. Applying (1) and (2), then taking (16) and (17) into
account, we obtain the relation (Sachs 1961)
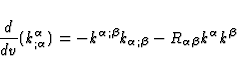
![\begin{displaymath}
\int \limits_{-\infty}^{v_{obs}} k^{\alpha}_{; \alpha} \verb...
... k^{\alpha} k^{\beta} +
k^{\alpha;\beta} k_{\alpha;\beta}] dv' \end{displaymath}](img73.gif)
![]() from the energy content of the regions crossed by the light
rays and from the geometry of the rays themselves.
from the energy content of the regions crossed by the light
rays and from the geometry of the rays themselves.
![]() (see e.g. Ellis 1971 or
Schneider et al. 1992). However, the corresponding formula will not be
useful for our discussion and we will not develop it here.
(see e.g. Ellis 1971 or
Schneider et al. 1992). However, the corresponding formula will not be
useful for our discussion and we will not develop it here.
![]() with respect to time. For this reason, it is more convenient to
calculate the total derivative of
with respect to time. For this reason, it is more convenient to
calculate the total derivative of ![]() along the world-line
along the world-line
![]() of a given observer, moving at the point x with the
4-velocity
of a given observer, moving at the point x with the
4-velocity ![]() .
.![]() the total
covariant differentiation along
the total
covariant differentiation along ![]() defined by
defined by
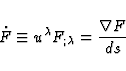
![]() is the energy of a photon
emitted by an
atom of the light source as measured by an observer comoving with this atom. So
is the energy of a photon
emitted by an
atom of the light source as measured by an observer comoving with this atom. So
![]() is a constant which depends only on the nature of
the atom (this constant characterizes the emitted spectral line). Consequently,
the change in the photon flux with respect to time is simply due to the change
in the scalar amplitude a and to the change in the spectral shift z.
From (24), we obtain at each point x of
is a constant which depends only on the nature of
the atom (this constant characterizes the emitted spectral line). Consequently,
the change in the photon flux with respect to time is simply due to the change
in the scalar amplitude a and to the change in the spectral shift z.
From (24), we obtain at each point x of ![]()
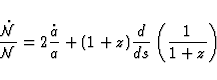
![]() in Eq.(33) the
geometrical scintillation because the variations in a are related to the
focusing properties of light rays by gravitational fields
(see G.F.R.Ellis 1971 and references therein; see also Misner et al.
1973).
in Eq.(33) the
geometrical scintillation because the variations in a are related to the
focusing properties of light rays by gravitational fields
(see G.F.R.Ellis 1971 and references therein; see also Misner et al.
1973).
![]() and
and ![]() in the
form of integrals along
in the
form of integrals along ![]() . In what follows, we assume that the ray
. In what follows, we assume that the ray
![]() hits at each of its points x(v) a vector field
hits at each of its points x(v) a vector field ![]() which
satisfies the boundary condition
which
satisfies the boundary condition
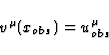
![]() may
be written as
may
be written as
![\begin{displaymath}
\left.\frac{\dot{a}}{a}\right\vert _{obs} = \int \limits_{-\infty}^{v_{obs}} \frac{d}{dv}
[v^{\mu}(\ln a)_{;\mu}] dv\end{displaymath}](img90.gif)
![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = k^{\alpha}( v^{\mu}
(\ln a)_{;\mu})_{;\alpha}\end{displaymath}](img91.gif)
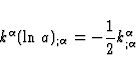
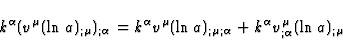
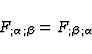
![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = v^{\mu} [k^{\alpha} (\ln
a)_{;\alpha}]_{;\mu} + [k,v]^{\mu} (\ln a)_{;\mu} \end{displaymath}](img95.gif)
![\begin{displaymath}[k,v]
^{\mu} \equiv k^{\alpha} v^{\mu}_{;\alpha} - v^{\alpha} k^{\mu}_{;\alpha}\end{displaymath}](img97.gif)
![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = -\frac{1}{2} v^{\mu}
k^{\alpha}_{;\alpha ;\mu} + [k,v]^{\mu} (\ln a)_{;\mu} \end{displaymath}](img98.gif)
![\begin{displaymath}
\frac{d}{dv} [v^{\mu}(\ln a)_{;\mu}] = \frac{1}{2} R_{\mu \n...
... v^{\mu} k^{\alpha}_{;\mu ;\alpha} +[k,v]^{\mu} (\ln a)_{;\mu} \end{displaymath}](img99.gif)
![]() in the form of an integral
along
in the form of an integral
along ![]() . In agreement with (27), we have at any point
x(v) of
. In agreement with (27), we have at any point
x(v) of ![]() :
:
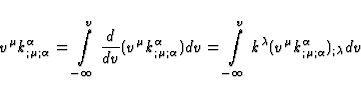
![]() is an arbitrary vector. So we can
choose
is an arbitrary vector. So we can
choose ![]() so that the transport equations
so that the transport equations
![[*]](foot_motif.gif)
![\begin{displaymath}[k,v]
^{\mu} = 0\end{displaymath}](img105.gif)
![]() along
along ![]() .
Henceforth, we suppose for the sake of simplicity that
the observer is freely falling, i.e. that
.
Henceforth, we suppose for the sake of simplicity that
the observer is freely falling, i.e. that ![]() is a timelike
geodesic. So we have
is a timelike
geodesic. So we have
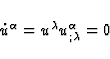
![]() is a constant characterizing the observed
spectral line (see above), it follows from (23) and (48) that
is a constant characterizing the observed
spectral line (see above), it follows from (23) and (48) that
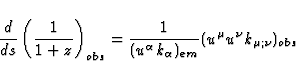
![]() fulfilling the boundary
condition (34), Eq.(49) may be written as
fulfilling the boundary
condition (34), Eq.(49) may be written as
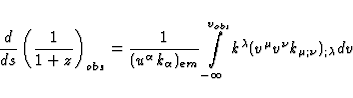
![]() the vector field defined by (46) and (34).
We obtain
the vector field defined by (46) and (34).
We obtain