Next: Conclusions Up: A hierarchical phasing algorithm Previous: Results
![]()
![]()
![]()
Next: Conclusions
Up: A
hierarchical phasing algorithm Previous: Results
The limiting magnitude estimates given by the early proponents of the sharpness criterion ([Muller & Buffington 1974,Dyson 1978]) were lower than those obtained in monolithic adaptive telescopes. This can be attributed to the intrinsic advantage of exploiting the wavefront continuity with analyser systems such as Shack-Hartmann ([Shack & Platt 1971]) or curvature sensing ([Roddier & Roddier C. 1991]). Long-baseline interferometers obviously cannot benefit from this advantage, but the triplet algorithm appears to improve somewhat the limiting magnitude with respect to the original sharpness algorithm.
Photon noise in the recorded image generates a speckled halo in its Fourier transform. The halo's addition to the correlation peaks affects their phase and intensity. With a photon-counting camera as the image detector, the Poisson statistics of the detected photons is preserved. If p photons are detected during a short exposure, the image's Fourier transform has a central peak having p times the average intensity of the halo. As in the high-level pattern, the intensity of the surrounding correlation peaks relative to the central peak is N-2 and further attenuated if the star is resolved. To have correlation peaks emerging from the halo p > N2 photons are thus needed, as required for reasonably accurate determination of the phases.
If the star is unresolved, the aperture phases can be calculated directly from the phases of the correlation peaks. Simulations with a simple iterative routine provided a fast convergence (2 or 3 iterations) and verified the p > N2 condition. This was achieved by subtracting from the phase of each aperture the average phase from the N correlation peaks related to the aperture, and iterating after recalculating the image's Fourier transform. In polychromatic light, the fractional excess method can be applied to the phases obtained in each correlation peak for deriving the optical path in each peak, and the routine then provides the optical paths of the apertures.
The 6-parameter optimisation of sharpness for each triplet requires
2 exposures for adjusting each parameter and thus 12 exposures. This requires
![]() detected photons from 9 apertures. Similarly, the full aperture stage requires
detected photons from 9 apertures. Similarly, the full aperture stage requires
![]() photons, hence a total of about p = 14000 within the life-time of
seeing. In practice fewer photons, about 800, proved enough to obtain rather
good images in our simulations of non-resolved objects, but resolved objects
are less favorable. This number also matches the p > N2
condition mentioned above for direct phase retrieval on un-resolved stars.
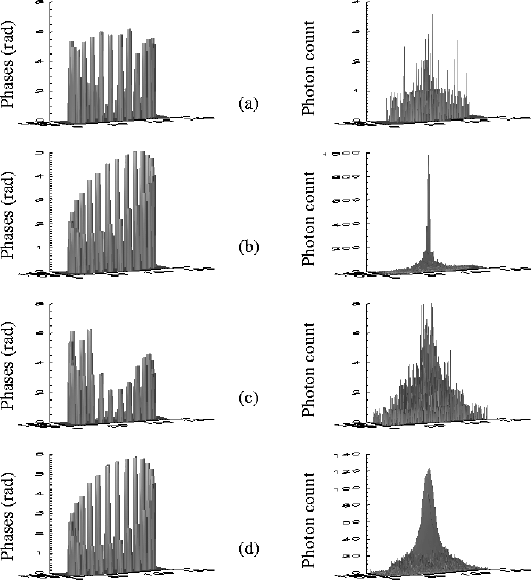
On a resolved object such as shown in Fig. 7.d,
130,000 photons were needed to obtain a Strehl ratio of 0.96 with a single
wavelength.
photons, hence a total of about p = 14000 within the life-time of
seeing. In practice fewer photons, about 800, proved enough to obtain rather
good images in our simulations of non-resolved objects, but resolved objects
are less favorable. This number also matches the p > N2
condition mentioned above for direct phase retrieval on un-resolved stars.
On a resolved object such as shown in Fig. 7.d,
130,000 photons were needed to obtain a Strehl ratio of 0.96 with a single
wavelength.
 |
With p photons received from the N-element aperture in time ![]() ,
corresponding to the life-time of seeing, the incident photon flux per
square centimeter B is:
,
corresponding to the life-time of seeing, the incident photon flux per
square centimeter B is: ![]() and the stellar magnitude
and the stellar magnitude ![]() ,
d being the size of the sub-aperture elements in centimeters,
,
d being the size of the sub-aperture elements in centimeters, ![]() the overall quantum efficiency, and
the overall quantum efficiency, and ![]() the bandwidth in Angström units. The limiting magnitude found with
27 apertures of 10cm, 0.02s seeing lifetime,
the bandwidth in Angström units. The limiting magnitude found with
27 apertures of 10cm, 0.02s seeing lifetime, ![]() and 300nm optical bandwidth is 5.4 with p=14000 photons and 8.3
with p=800 photons, somewhat higher than the value 4.3 found by
Muller et al. in identical conditions.
and 300nm optical bandwidth is 5.4 with p=14000 photons and 8.3
with p=800 photons, somewhat higher than the value 4.3 found by
Muller et al. in identical conditions.
Large sub-apertures with uniform phase, obtainable with a number of large ground-based telescopes equipped with adaptive optics and a laser star, can push the limiting magnitude for inter-aperture phasing towards mv=20, assuming 10m telescopes. The intra-aperture adaptive optics increases the lifetime of the wavefront's phase, owing to its averaging effect, and this contributes to the magnitude gain.
In space, much longer lifetimes can be expected, given the excellent predictability and measurability of telescope motions in the quiet micro-gravity environment. The availability of reference stars also favors efficient phasing on very faint objects. As discussed elsewhere ([Labeyrie 1998]), the extreme case of 100,000 km optical baselines dedicated to observations of neutron stars appears manageable in terms of phasing. A more detailed analysis of limiting magnitudes with various array configurations, object shapes and phasing methods is desirable.