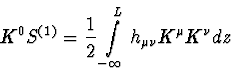
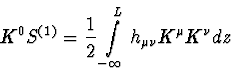 |
(104) |
L'onde électromagnétique est décrite par son vecteur d'onde
![]() où K0 est une constante.
où K0 est une constante.
Au point courant M où le rayon rencontre l'onde
gravitationnelle (cf Fig.D.1), ![]() s'écrit dans le référentiel
local (x',y',z') de l'onde gravitationnelle
s'écrit dans le référentiel
local (x',y',z') de l'onde gravitationnelle
| (105) |
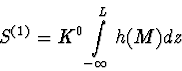 |
(106) |
| (107) |
Le terme en ![]() traduit le
caractère tensoriel transverse de l'onde gravitationnelle: les
photons qui voyagent dans la direction de l'onde gravitationnelle (
traduit le
caractère tensoriel transverse de l'onde gravitationnelle: les
photons qui voyagent dans la direction de l'onde gravitationnelle (![]() )
ne subissent aucun effet alors que l'effet est maximal pour une interaction
tangentielle (
)
ne subissent aucun effet alors que l'effet est maximal pour une interaction
tangentielle (![]() ).
).
Conformément à la Fig.D.1, lorsque l'axe de rotation du système
est dans le plan du ciel de l'observateur, les rayons lumineux contenus dans le
plan de l'orbite interagissent avec des ondes gravitationnelles pour
lesquelles ![]() . En reportant (B.21) dans (D.4), il
vient
. En reportant (B.21) dans (D.4), il
vient
| (108) |
L'analyse détaillée des perturbations de phase optiques est désormais menée dans cette configuration particulière. Le calcul reste cependant suffisamment général pour décrire le comportement global des déformations de phases optiques.
L'origine des temps est fixée à la traversée du plan (xy). Les rayons lumineux rencontrent en M, à la distance z de ce plan, une onde gravitationnelle émise au temps r/c antérieur. La différence de phase est donc proportionnelle à z-r. Compte tenu de (D.5), (D.3) devient
![\begin{displaymath}
S^{(1)}(\rho, \phi_0) = \frac{1}{2} K^0 \gamma \rho^2 \int \...
...nfty}^{L}
r^{-3} \cos [2 \pi \lambda_g^{-1} (z-r) + \phi_0] dz\end{displaymath}](img221.gif) |
(109) |
La relation (D.6) correspond à la relation établie par
A.Labeyrie (1993)
pour les déformations géométriques W(1) d'un plan d'onde optique
engendrées par des ondes gravitationnelles.
Le calcul détaillé qui a été présenté montre cependant que cette
relation décrit en fait les déformations de phase optiques, qui
prennent en compte d'éventuelles variations spectrales (cf. C![]() 5).
5).