


Next: Discussion.
Up: Rapport à la méthode
Previous: Déformation du front d'onde.
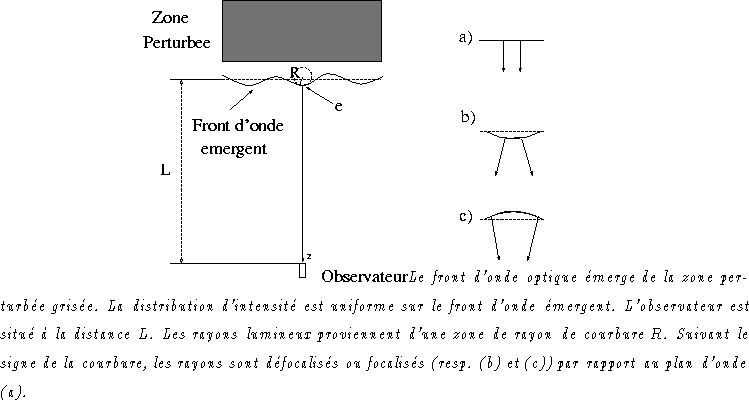
La région grisée Fig.C.3 représente une perturbation
localisée. La distribution d'intensité I0 sur le front d'onde
est constante à la sortie de la zone perturbée. Cette distribution
évolue ensuite au cours de la propagation.
L'observateur est situé à la distance L de la zone d'interaction.
Les rayons lumineux reçus par cet observateur proviennent d'une zone qui
découpe un arc de longueur e sur le front d'onde optique déformé,
dans le plan de la Fig.C.3. Soit R le rayon de courbure local du front
d'onde et a le diamètre du télescope.
En assimilant les arcs à des segments, il vient
| 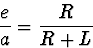 |
(92) |
Figure:
 |
Pour une perturbation dynamique, les déformations des fronts
d'onde optique successifs évoluent de même que la courbure des zones
envoyant les rayons à l'observateur.
En définissant la courbure par C=1/R, la différentielle logarithmique
de l'expression précédente conduit à
| 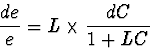 |
(93) |
Dans le cas où la courbure sagittale peut être négligée, i.e.
où la déformation est quasiment de révolution,
l'intensité mesurée par l'observateur est directement proportionnelle au
flux passant à travers l'élément de longueur e et la modulation
d'intensité à l'observateur est, pour de petites déformations
| 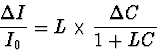 |
(94) |
où 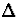 symbolise la variation entre deux instants d'observation
associés aux dates ti et ti+1 pour lesquelles les fronts d'onde
optique présentent les déformations W(1)i et W(1)i+1
respectivement.
C devient la courbure totale du front d'onde lorsque intervient la courbure
sagittale.
symbolise la variation entre deux instants d'observation
associés aux dates ti et ti+1 pour lesquelles les fronts d'onde
optique présentent les déformations W(1)i et W(1)i+1
respectivement.
C devient la courbure totale du front d'onde lorsque intervient la courbure
sagittale.
Dans l'approximation des faibles déflexions la courbure se
réduit à la dérivée seconde du profil du front d'onde.
Le terme au dénominateur de (C.66) doit être pris en compte dans le cas
d'une courbure statique sur laquelle viennent se greffer les perturbations.
En l'absence d'une telle déformation statique la relation (C.66) s'écrit
| ![\begin{displaymath}
\frac{\Delta I}{I_0}= L.\Delta \left( [\frac{\partial^2}{\pa...
...l x^2}
+ \frac{\partial^2}{\partial y^2}] W^{(1)}_i(x,y)\right)\end{displaymath}](img193.gif) |
(95) |
À la sortie de la perturbation, les déformations W(1)i(x,y) se
propagent librement sur la distance L. La relation (C.67) s'écrit donc
également
| ![\begin{displaymath}
\frac{\Delta I}{I_0}= \Delta \left( \int \limits_{z_2}^{z_2+...
... + \frac{\partial^2}{\partial y^2}]
W^{(1)}_i(x,y)
dz \right) \end{displaymath}](img194.gif) |
(96) |
W(1) étant indépendant de z et t pour un front
d'onde optique donné, la relation précédente s'écrit aussi
| 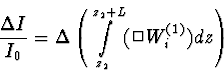 |
(97) |
où l'opérateur 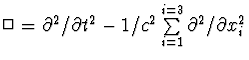 est le d'Alembertien ordinaire.
est le d'Alembertien ordinaire.
Voyons comment cette relation se rapproche de (C.18).
Pour une onde plane électromagnétique sur un espace-temps plat,
l'intégrant de (C.18) donne, dans le cas des faibles perturbations
|  |
(98) |
où a(0) est constant.
La variation géométrique de l'intensité est liée à la
variation du carré de l'amplitude scalaire soit
| 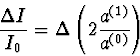 |
(99) |
L'intégration est menée le long du trajet non perturbé
du rayon lumineux, i.e. une ligne droite de l'espace plat.
Le paramètre affine v de (C.12) est alors lié au temps propre de
l'observateur par
| 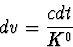 |
(100) |
que l'on identifie à
| 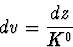 |
(101) |
avec un choix particulier du système de coordonnées pour lequel l'axe des
z est parallèle à la direction de propagation des rayons lumineux.
D'où
| 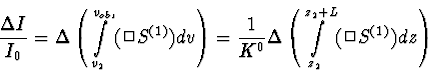 |
(102) |
Identifier (C.74) et (C.69) revient à identifier au facteur multiplicatif
K0 près 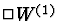 et
et 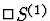 .
Les déformations W(1)i, d'après la définition (C.63), ne prennent
en compte que les variations géométrique de chemin optique. Ces variations
ne sont égales
aux variations de S(1)/K0 qu'à un terme
.
Les déformations W(1)i, d'après la définition (C.63), ne prennent
en compte que les variations géométrique de chemin optique. Ces variations
ne sont égales
aux variations de S(1)/K0 qu'à un terme 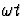 près, où
près, où
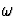 est la pulsation du rayonnement électromagnétique. Si la
perturbation n'engendre pas de variations temporelles de
est la pulsation du rayonnement électromagnétique. Si la
perturbation n'engendre pas de variations temporelles de 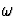 , une
hypothèse admissible classiquement, alors
, une
hypothèse admissible classiquement, alors
| 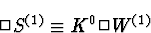 |
(103) |
et les deux méthodes pour évaluer la scintillation convergent
naturellement.



Next: Discussion.
Up: Rapport à la méthode
Previous: Déformation du front d'onde.
11/13/1998
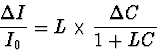
![\begin{displaymath}
\frac{\Delta I}{I_0}= L.\Delta \left( [\frac{\partial^2}{\pa...
...l x^2}
+ \frac{\partial^2}{\partial y^2}] W^{(1)}_i(x,y)\right)\end{displaymath}](img193.gif)
![\begin{displaymath}
\frac{\Delta I}{I_0}= \Delta \left( \int \limits_{z_2}^{z_2+...
... + \frac{\partial^2}{\partial y^2}]
W^{(1)}_i(x,y)
dz \right) \end{displaymath}](img194.gif)
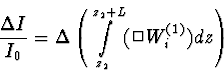
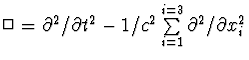 est le d'Alembertien ordinaire.
est le d'Alembertien ordinaire.
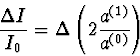
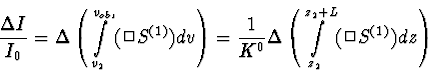
![]() et
et ![]() .
Les déformations W(1)i, d'après la définition (C.63), ne prennent
en compte que les variations géométrique de chemin optique. Ces variations
ne sont égales
aux variations de S(1)/K0 qu'à un terme
.
Les déformations W(1)i, d'après la définition (C.63), ne prennent
en compte que les variations géométrique de chemin optique. Ces variations
ne sont égales
aux variations de S(1)/K0 qu'à un terme ![]() près, où
près, où
![]() est la pulsation du rayonnement électromagnétique. Si la
perturbation n'engendre pas de variations temporelles de
est la pulsation du rayonnement électromagnétique. Si la
perturbation n'engendre pas de variations temporelles de ![]() , une
hypothèse admissible classiquement, alors
, une
hypothèse admissible classiquement, alors