Abstract. The fibre-fed echelle spectrograph of Observatoire de
Haute-Provence, ELODIE, is presented. This instrument has been in operation
since the end of 1993 on the 1.93m telescope. ELODIE is designed as an updated
version of the cross-correlation spectrometer CORAVEL, to perform very accurate
radial velocity measurements such as needed in the search, by Doppler shift,
for brown-dwarfs or giant planets orbiting around nearby stars. In one single
exposure a spectrum at a resolution of 42000
(![]() /
/![]()
![]() )
ranging from 3906Å to 6811Å is recorded on a 1024x1024 CCD. This
performance is achieved by using a tan
)
ranging from 3906Å to 6811Å is recorded on a 1024x1024 CCD. This
performance is achieved by using a tan![]() = 4 echelle grating and a
combination of a prism and a grism as cross-disperser. An automatic on-line
data treatment reduces all the ELODIE echelle spectra and computes
cross-correlation functions. The instrument design and the data reduction
algorithms are described in this paper. The efficiency and accuracy of the
instrument and its long term instrumental stability allow us to measure radial
velocities with an accuracy better than 15 m s-1 for stars up to 9th
magnitude in less than 30 minutes exposure time. Observations of 16th magnitude
stars are also possible to measure velocities at about 1 km s-1
accuracy. For classic spectroscopic studies (S/N>100) 9th magnitude stars
can be observed in one hour exposure time.
= 4 echelle grating and a
combination of a prism and a grism as cross-disperser. An automatic on-line
data treatment reduces all the ELODIE echelle spectra and computes
cross-correlation functions. The instrument design and the data reduction
algorithms are described in this paper. The efficiency and accuracy of the
instrument and its long term instrumental stability allow us to measure radial
velocities with an accuracy better than 15 m s-1 for stars up to 9th
magnitude in less than 30 minutes exposure time. Observations of 16th magnitude
stars are also possible to measure velocities at about 1 km s-1
accuracy. For classic spectroscopic studies (S/N>100) 9th magnitude stars
can be observed in one hour exposure time.
ELODIE is the new fibre-fed echelle spectrograph of the 1.93m-telescope of Observatoire de Haute-Provence (OHP), France. It was put into operation at the end of 1993. This instrument has been designed for three different observing objectives :
The efficiency of cross-correlation spectroscopy for radial velocity measurements of late-spectral-type stars (Griffin 1967, Baranne et al. 1979) is well established, but the experience gained with the two CORAVEL since 1977, at the OHP and La Silla Observatories, has shown the limitations of this technique when using a slit spectrograph and a physical template. In particular, the instrumental accuracy is limited to some 200 ms-1 (Duquennoy & Mayor 1991a). This considerably limits the possibility of searching for giant planets or brown dwarfs orbiting around stars. This important limitation is mainly due to errors introduced by the variable illumination of the entrance slit (guiding, focus, variable optical axis of the telescope and calibration lamp, etc.). See Griffin & Griffin (1973) for a discussion of classical difficulties affecting radial velocity measurements. The fixed geometry of the CORAVEL template, being calculated for a well defined air-refractive index, also produces wavelength shifts which are not fully compensated by the zero-point shift determined by the calibration lamp.
The difficulties related to the fixed geometry of the mask used in the optical cross-correlation technique are fully removed with the numerical correlation. Another advantage of the numerical cross-correlation is the possibility of building different templates adapted to different spectral types or measurement goals (see below). An important gain is also expected in the limiting magnitude due to the much better quantum efficiency of the CCD compared to a photomultiplier, and also by avoiding the sequential scanning needed to build the cross-correlation function in CORAVEL-type instruments. In fact, the loss of efficiency due to the scanning is about a factor ten (the ratio between the scanning span and the width of the entrance slit). However, some loss of efficiency is expected from the much larger noise per pixel of the CCD compared to the noise of a single photo-electric detector.
Instruments specialized in precise Doppler shift measurements, in operation for more than a decade, reach accuracies of about 20 m s-1 (Campbell & Walker 1979, Cochran 1988, Cochran & Hatzes 1990, McMillan et al. 1990, Marcy et al. 1993, Murdoch et al. 1993). Most of these instruments include an absorption cell in front of the spectrograph (HF or iodine cell) to superimpose absorption lines on the stellar spectrum. That solution prevents errors caused by different optical paths crossed by the stellar beam and the calibration lamp beam. But, with these instruments, only bright stars have been monitored due to the very high signal-to-noise ratio required for high precision Doppler measurements. As a result, only limited samples of stars in the solar vicinity have been measured and no detection of Jupiter-size planets has been reported (Marcy & Butler 1994, Walker et al. 1995).
The option chosen for ELODIE does not make use of an absorption cell
in front of the spectrograph. The problem of the illumination of the
entrance slit and collimator is almost completely eliminated by using an
optical fibre to feed the spectrograph (Heacox 1986). This also allows us
the design of a fixed position spectrograph in an isothermal environment.
The condition of identical path for star and calibration is also provided
by the high stability and the scrambling effect of the optical fibre.
However, long term thermal relaxation of the spectrograph as well as air
pressure variations induce non negligible drifts in the spectrograph. An
accuracy of a few meters per second is only possible if a simultaneous
calibration is done. ELODIE has two fibres (one for the star, the other for
the sky). Tests and measurements carried out during the first year of
operation have revealed that the relative drift between the sky spectrum
and the star spectrum is highly correlated. Therefore, we use the sky fibre
illuminated by the thorium-argon lamp during the stellar exposure to
monitor the spectrograph calibration variation. The results reported in the
last section of this paper indicate that a similar accuracy to that of
the absorption cell instruments is achieved. To increase the long term
stability of ELODIE, a fixed optical system has been chosen,which certainly
introduces some limitations for spectroscopy. However, the available
wavelength range is wide (~ 3000Å). It allows the simultaneous
measurement of calcium H and K lines and of the hydrogen H![]() line.
line.
While ELODIE has been carefully designed to be able to provide accurate radial velocities on a long time span (Jupiter-size planets and brown dwarf searches) as well as on very short time (asteroseismology), it is also true that this instrument is perfectly suited to the measurement of fairly accurate radial velocities (1 km s-1 ) of very faint stars. Such a domain of application is certainly promising. Cross-correlation spectroscopy also offers an efficient way of measuring rotational velocities of late-spectral type stars (Benz & Mayor 1981, 1984) and the stellar metallicities of faint stars (Mayor 1980, Pont et al. 1995b). But more can be extracted from spectra if specific templates are designed by using one's a priori knowledge of stellar spectra, a field for future developments with any high resolution echelle spectrograph. For example, the comparison of cross-correlation functions computed with the same spectrum but using different sets of spectral lines of increasing Landé factors can reveal some information on the surface magnetic field of stars (Babel et al. 1995, Queloz et al. 1996).
A crucial aspect of optical cross-correlation instruments is their capacity to provide instant measurements of radial velocity. An important software development has been done to preserve this aspect and to provide a complete on-line reduction of the CCD frames, giving access to the calibrated spectrum and its radial velocity a few minutes after the end of the exposure. The main features of the software are described in this paper.
ELODIE is an Haute-Provence Observatory instrument designed and built in the context of a collaboration between the Haute-Provence, Marseille and Geneva Observatories. A second copy of this spectrograph, called CORALIE, will be located on the new 1.2-meter telescope to be installed at la Silla Observatory (ESO, Chile) by the Geneva Observatory.
A general description of the instrument is presented in the next section. The main features of the reduction software are outlined in section 3. Section 4 is dedicated to the first results and the performances of the instrument. ELODIE as part of the accelerometer instrument designed by Connes (1985), being still under development, is not described here.
In an astronomical spectrograph the camera aperture diameter is larger than the disperser size and increases according to the field size. Thus, it is quite impossible to have a high aperture ratio for the camera if a large and very dispersive grating is used.
On the contrary, this limitation does not exist in the "white pupil" mountings: the disperser is re-imaged on the camera and monochromatic beams intersect each other in the new pupil which has to be superimposed on the camera entrance. The magnification between these two pupils (disperser and camera) is a free parameter which has to be chosen in accordance with the camera's optical properties, but the camera size is independent of the disperser size.
In all previously described "white pupil" mountings a more or less complex dioptric system (i.e. a double-pass Littrow collimator) gives, when a reflexion grating is used, a first intermediate spectrum in the vicinity of the slit. In this intermediate space, transfer optics which provide "white pupil" conjugation can either be used as simple field optics, which doesn't change the Littrow aperture, or as a second collimator for another (cross) disperser needing parallel light illumination.
The absence of constraints in the choice of transfer optics leads to a large variety of mountings which share some useful properties:
The echelle-grating used has a
tan![]() = 4 (
= 4 (![]() = 76°) blaze
angle. It is a very impressive optical component (408x102mm with 31 g
mm-1) produced by Milton Roy. Using a TK1024 CCD with 24 µ pixels
as detector we record, in one single exposure, a spectrum from 3906Å to
6811Å distributed over 67 orders. The focal length of the camera is
adjusted to avoid any gap in this range and to record all the wavelengths even
in the extreme red orders. This leads to a focal length of 300 mm, an aperture
ratio f/3 and a reciprocal linear dispersion of 2 Å/mm in the middle of
the range (4800Å).
= 76°) blaze
angle. It is a very impressive optical component (408x102mm with 31 g
mm-1) produced by Milton Roy. Using a TK1024 CCD with 24 µ pixels
as detector we record, in one single exposure, a spectrum from 3906Å to
6811Å distributed over 67 orders. The focal length of the camera is
adjusted to avoid any gap in this range and to record all the wavelengths even
in the extreme red orders. This leads to a focal length of 300 mm, an aperture
ratio f/3 and a reciprocal linear dispersion of 2 Å/mm in the middle of
the range (4800Å).
The spectrograph is made up of two levels. Used in the Littrow condition but in conic dispersion the echelle grating is put at the common focus of both adjacent mirrors M1 and M2 (see Fig. 1 for a display). It forms the pupil of this Czerny-Turner mounting which constitutes the first level of the spectrograph. An intermediate spectrum is observed in a position symmetrical to the source in relation to the grating. This first spectrum is itself constituted by all the overlapping orders which will be disentangled in the second level.
With a fibre-fed spectrograph, the collimator focal ratio is a free parameter (in so far as adecquat transfert optical systems make numerical aperture between fibre and collimator fitted together, see below). We chose f/15 in order to prevent off-axis effects. The intermediate spectrum lies in a telecentric space. It appears rectilinear in the sagittal focal surface which is plane. The spherical aberration is negligible due to the small aperture angle, and there is no coma thanks to the Z Czerny-Turner mounting. In fact, the only aberration we observe is the same astigmatism for all wavelengths coming from the off-axis illumination of M1 and M2.
A small mirror near the intermediate spectrum sends back the monochromatic beams towards a third concave mirror M3 adjacent to the Czerny-Turner mirrors. This third mirror is a new collimator for all these beams which, after the mirror and at its focus, forms a "white pupil" in parallel light. This pupil is the white image of the echelle-grating (diameter 102 mm) but reduced to a diameter of 75 mm, which is more than enough to obtain a good correction of aberrations. It is worth noticing that the Z-mounting between pupils also reduces the pupilar coma.
The dispersion crossing is done by a pair of dispersers, the first being a prism, the second a grism (one deals with the subject as it is currently done for chromatism). All beams traverse first a 40° flint prism, then an 8.63° crown grism with 150 g mm-1. Both dispersers work at minimum deviation. Note that, if the separation of the orders were done only by a prism we would notice more space between blue orders than between red ones. If, on the contrary, the separation were done by a grism, more space would be observed between the red orders. Using these two effects together we have a constant inter-order spacing over the whole wavelength range, and we record 67 orders on our 1024x1024 CCD (see Fig. 2).
2.2.1. Camera
From the above, one might think that the only aberration which will be observed at the focus of a camera computed for infinity would be off-axis astigmatism. In fact, being the same for all image points, this astigmatism is corrected by an appropriate toroidal deformation on the optical surface very close to the pupil. In ELODIE the object field is very small, and it is therefore easy to make this deformation on the first mirror M1. The camera has therefore been computed for an aberration-free field at infinity. Its aperture is f/3 with a diameter of 75 mm. (The camera's real focal length of 225 mm has to be taken into account in calculating the cross-dispersion, but the pupil magnification affects the calculation of the main dispersion since (as we have seen above) the equivalent focal length is 300 mm. )
The small cylinder effect observed in the field, due to the crossing of prisms, is corrected by adjusting the secondary chromatism in the camera. The ELODIE potential resolution is about 100000 (see the spot-diagrams in Fig. 3).
Note that a removable rocking parallel plate (UBK7/20 mm) is installed inside the camera in order to move the image without degrading the optical quality of ELODIE. This equipment is a part of the accelerometry instrument of Connes.
2.2.2. Parasitic orders and filters
As we have seen, with a single 1024x1024 CCD, a 3000Å wavelength range is recorded at one time with a maximum resolution of 100000. The optical system required to obtain this result is rather complex and has numerous surfaces. The difficulties which this entail must be solved with care.
The first difficulty is a standard problem. The transmission has to be best within the useful wavelength range and reduced as much as possible outside this band. This passband function is obtained by a combination of extra-low reflection coatings on the glasses and special dielectric mirrors.
The second difficulty is unusual and more tricky to handle. The crossed dispersion is accomplished by two components: the prism and the grism, whose effects are added. The first order of the grism is used, but wavelengths in this order are already widely dispersed by the prism, as well as the wavelengths in orders 0 and 2. Thus, on the blue part of the CCD appear red wavelengths, while on the red side of the echelle spectrum, the blue wavelengths of order 2 are visible. The rejection of the unwanted orders of the cross-disperser is done by a filter with two coatings inserted in front of the CCD. The first filter, a short-wavelength pass filter, is located on the blue side of the echelle spectrum and the second, a long-wavelength pass filter, is located on the red side. These two additional filters are not adjacent, because the central part of the spectrum is not polluted. As the CCD is much more sensitive in the red, a short-wavelength pass filter is also added at the entrance of the spectrograph. This filter, combined with the dielectric mirrors, increases the efficiency of the short-wavelength pass filter (only below 7000Å). It is worth adding that the two sides of these filters, as well as the other diopters of the spectrograph, are also coated with an extra-low reflection coating.
The transmission of the whole useful wavelength range is not particularly influenced by these additional filters. The filters are also located far enough from the CCD to avoid any photometric effect at the limit of the coated areas. However the location of the long-wavelength pass coating does not match perfectly all the area contaminated by the wavelengths of the order 2. Therefore a slight blue contamination remains in the middle of the CCD (see Fig. 11 below)
An adaptor, located at the f/15 Cassegrain focus, and two optical fibres provide the optical link between the telescope and the spectrograph, which is kept in an isolated room. The front-end adaptor is composed of many mechanisms. It holds the calibration lamps, does the correction for atmospheric differential refraction and permits the stellar field visualization and the guiding (see Fig. 4).
2.3.1. Stellar field visualization and guiding
A tilted steel concave mirror pierced with two holes of 300 µ diameter (2 arcsec on the sky) allows the fibres to be fed and, at the same time, the image of the field to be reflected onto the guiding camera. These holes are hereafter called : star-hole and sky-hole.
A shutter in front of the camera and a density wheel are also available to protect the guiding camera during the setting of the telescope and the calibration exposures. The automatic guiding is done on the video image.
2.3.2. Calibration exposures
The beam coming from the calibration sources is separated so as to obtain two distinct ways keeping the same pupil. This optical design is highly diffuseless and allows short exposure times. It also prevents the scattered light of the calibration lamp from reaching the guiding camera and the star-hole during a simultaneous exposure on a star (simultaneous thorium).
Several types of calibrations are provided by the adaptor, (see also Table 1 for a summary of all the combinations):
Table 1.
List of all possible exposure combinations
using the calibration lamps.
--------------------------------------------------------------
calibration type star-hole sky-hole
--------------------------------------------------------------
1 tungsten tungsten
2 thorium-argon thorium-argon
3 star thorium-argon
4 Fabry-Perot Fabry-Perot
4 star Fabry-Perot
4 thorium-argon Fabry-Perot
--------------------------------------------------------------
This system limits as much as possible the loss of star light by the differential atmospheric refraction at the entrance of the fibre. In term of performances such a system is less demanding than would be, for instance, a speckle image system. However, it must not reduce the size of the field for the setting.
The atmospheric dispersion correction is done with a set of four normal field prisms and a parallel plate. As the coma coming from the use of the convergent beam before the Cassegrain focus of the telescope is negligible, this solution is very convenient and provides good transmission. The choice of the prism set is done so that the secondary spectrum never exceeds 0.3 arcsec in length up to a sec z = 2 telescope position.
We use POLYMICRO fibres FHP, 20 meters long, with a diameter of 100 µ (Avila 1988). Our choice is to form the star image and not the pupil on the fibre entrance. Note that it would be interesting to compare the quality of both solutions in term of efficiency and radial velocity accuracy. The beam apertures are converted to f/5 with a transfer optic to feed the fibres and then brought back to f/15 at the spectrograph entrance. In the end, at the focus of the f/3 camera lens, the geometrical spot diameter is 60 µ. Therefore the effective resolution of ELODIE is about 40000.
The main difficulty in the fibre mounting comes from the optic cable SMA connectors. The final quality remains strongly dependent on the overall assembly. We have designed a device to control the conservation of the input-output numerical aperture of fibres. The method consists in illuminating the entrance of the fibre with a beam of fixed aperture (here f/4.5) and to analyse the flux at the end of the fibre through a diaphragm of variable aperture. On Fig. 5 we see that it is possible to obtain a final transmission close to the optimum, limited only by the loss in the glass and the air-glass interface.
An exposure meter records continuously the flux which enters the spectrograph. This information is very helpful in selecting the optimum observing time. Furthermore, this allows us to compute the true mean time of the exposures, which is critical for accurate correction for the Earth's velocity. Note that the variation of the radial projection of the Earth's motion on the line of sight, at OHP, can be as large as 1.5 m s-1 min-1.
The exposure meter is fed by the light out of the efficient beam, as near as possible to the blaze. A spherical mirror (aperture f/1) located on the normal side of the grating and a bundle of optical fibres lead the light to a photomultiplier outside the spectrometer. We have measured that 3% of the light entering in the spectrometer reaches the photomultiplier. It is worth noting that we tried another method consisting in collecting the light of low and grazing orders but only collected 0.3% of the incoming flux.
A back-side illuminated TK1024 with 24 µ pixels is used. It is cooled to 183 K. Particular attention is given to the temperature regulation in order to insure good stability. At this temperature, using a slow read out (100 us/pixel), we measure a typical read-out noise of 8.5 e-. The CCD quality is typical of a grade 1 and its linear response is excellent up to 100000 e-. Four gains are available: 4, 2, 0.8 and 0.4 e-/ADU.
Five computers are used to control the instrument:
All these computers are connected via an Ethernet network. They communicate using the client-server protocol.
The use of ELODIE is fully automatic, no manual action is needed to configure the spectrograph and carry out the observations. A specific user interface is used by the observer to start the exposures. All the actions are then automatically realized up to the end of the data reduction. The "pipeline" includes the exposure configuration, the exposure itself, the data acquisition and the reduction. The stellar exposures are defined by their exposure times but, thanks to the exposure meter, a signal-to-noise ratio to be achieved can also be requested.
The sequence of exposures i treated simultaneously, as a stack, along the pipeline in order to spare as much time as possible. The maximum stack available by the system is the following: an exposure in the reduction program; an exposure waiting for reduction; the exposure in progress and an exposure defined, ready to be started.
The use of fibres to feed the spectrograph makes the position and the shape of the orders stable on the CCD and independent of the seeing. Therefore, it is possible to define an optimum data reduction procedure and to apply this treatment algorithm, in an automatic way, for all the spectra observed. Such a program, specifically adapted to the instrument, provides a set of homogeneous spectra and saves the observer the labour of reducing the echelle spectra.
An automatic on-line data treatment, completely integrated in the spectrograph operation train, is available with ELODIE. The images are reduced directly after the exposures. Considering the quality of the algorithms used, the ELODIE reduction must not be seen as a quick look facility but as a extension of the spectrograph abilities, providing reduced data instead of "classical" CCD raw images.
The work itself is done with an interpreter, dedicated to the fast treatment of astronomical images (Weber 1996, in preparation). A set of specific algorithms has been developed in this environment to reduce echelle spectra.
All the images coming from the spectrograph are saved on a disk for security purposes. The classical treatment of CCD frames is then carried out: correction of bad pixels, offset and dark current subtraction. Note that, as the offset and the dark are not constant over the CCD, averages of 64x64 pixels are used, for both images, instead of a single average value.
The determination of the position of the orders is achieved by illuminating the fibre entrances with the tungsten lamp. The geometrical definition of the sky orders and star orders are carried out in two distinct exposures. From these images, the orders are geometrically characterized and the blaze function and the flat-field spectrum are also computed.
The wavelength calibration is done with the thorium lamp. After the extraction of the orders, the thorium emission lines are identified on the spectrum and the wavelength geometry is fitted using a two-dimensional polynomial expansion of the Littrow approximation for the echelle grating solution. The quality of the solution is finally controlled by computing the cross-correlation function of the thorium spectrum. The focus of the spectrograph is also checked during this operation.
A "true" flat-field image with widened orders is available with ELODIE. The width of the orders is artificially increased by changing the position of the image of the fibre entrance in the spectrograph. This image, called flat-field image, (not to be confused with the flat-field spectrum) gives after some treatment the relative response of the pixels in the direction perpendicular to the dispersion (Y-direction) for each order and at each resolution bin along the main dispersion (X-pixels). The response of the pixels along the main dispersion is given by the flat-field spectrum. It is computed from the extracted spectrum of a tungsten exposure (not broadened) previously divided by the flat-field image (before the extraction). For all the stellar exposures, the flat-field correction is then made in two steps: first dividing the image by the flat-field image and then the extracted spectrum by the flat-field spectrum. Note that this correction in two steps is not necessary for spectra with S/N < 300.
Three stellar exposure types are available (see Fig. 6) : (1) "star fibre only": the fibre mask is set on the sky-hole; (2) "star fibre and sky fibre": the fibre mask is out of the telescope beam in order to measure the sky spectrum as well; (3) "simultaneous thorium": during the exposure, the thorium lamp illuminates the sky fibre to monitor the spectrograph drift.
The observations of relatively bright stars, requiring careful spectroscopic reduction, is done with "star fibre only" exposures. The inter-order spacing is large enough carefully to estimate the background contamination and to correct for it. In the case of faint objects, which can be significantly contaminated by the skylight, a "star fibre and sky fibre" exposure is to be preferred. For such an image however, as the orders are too close, no background subtraction is possible. For both exposure types, the orders are then extracted and wavelength calibrated using the last thorium exposure carried out.
For the simultaneous thorium exposure, the thorium spectrum is extracted, calibrated with the last thorium exposure and then cross-correlated. The wavelength solutions of each way (sky and star) are independent but their drifts are similar (see part 4.1). Therefore, the velocity shift of the sky spectrum corresponds to the measurement of the mean spectrograph drift relative to the last wavelength calibration. As for the "star fibre and sky fibre" exposure there is no background subtraction.
For all the exposure types, the observer has the possibility of computing cross-correlation functions. The algorithm uses "binary" templates and mimics the CORAVEL process (e.g. Baranne et al. 1979, Queloz 1995b).
The geometrical definition of the orders starts with the
search for the order location in the middle of the image along a column (in
the Y-direction). Then, the algorithm computes the centre of gravity yc of
each order at every x position, moving step by step from the centre to the
edges of the image. Finally, a two dimensional polynomial is fitted to
constrain the order location: 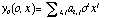 ,
where o is the order number (internal numbering) and x the pixel position. To
get a g ood solution out to the edges of the image, a high signal-to-noise
ratio spectrum is used and the image background is carefully subtracted. On
Fig. 7 the position of the orders found by the algorithm, in the four corners
of the image, is displayed.
,
where o is the order number (internal numbering) and x the pixel position. To
get a g ood solution out to the edges of the image, a high signal-to-noise
ratio spectrum is used and the image background is carefully subtracted. On
Fig. 7 the position of the orders found by the algorithm, in the four corners
of the image, is displayed.
The shape of the orders perpendicular to the dispersion (spatial profile) is approximated by a Gaussian. To fit this shape throughout the image, a set of 2-dimensional functions (called herein after elongated Gaussians) is used:
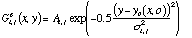
Each of these functions is fitted over a range of 30 X-pixels with the
width (![]() ) and the amplitude (A) as free
parameters. The previous determination of the position of orders (y
c(x,o))
is used. The si,j measured are then fitted with a two-dimensional polynomial
to give a continuous description
) and the amplitude (A) as free
parameters. The previous determination of the position of orders (y
c(x,o))
is used. The si,j measured are then fitted with a two-dimensional polynomial
to give a continuous description ![]() (x,o) of
the width of the orders throughout the image. This algorithm provides a
good description of the spatial profile, independent of the order position.
The use of elongated Gaussians in the X direction instead of several
Gaussians permits strongly to decrease the pixel sampling noise and
increases the quality of the measurement. This is particularly important for
ELODIE which has narrow and very slightly tilted orders. Figure 8 displays
the comparison between the observed profile and the fitted model. One
clearly sees that a Gaussian shape is a good approximation to the spatial
profile for a fibre-fed spectrograph.
(x,o) of
the width of the orders throughout the image. This algorithm provides a
good description of the spatial profile, independent of the order position.
The use of elongated Gaussians in the X direction instead of several
Gaussians permits strongly to decrease the pixel sampling noise and
increases the quality of the measurement. This is particularly important for
ELODIE which has narrow and very slightly tilted orders. Figure 8 displays
the comparison between the observed profile and the fitted model. One
clearly sees that a Gaussian shape is a good approximation to the spatial
profile for a fibre-fed spectrograph.
The comparison between the true profile and its adjustment gives a good estimate of the error in the position of the orders found by the program. As the centre is not a free parameter during the fit of the elongated Gaussian, any mismatch would have a direct consequence on the quality of the fit. After some investigations we concluded than if any systematic error greater than 1/10 pixel were present it would be clearly visible.
The variation of the width of the orders across the image, displayed in Fig. 9, shows that the focus perpendicular to the main dispersion is sharper in the red part than in the blue part of the image and that there is a slight effect along each order. The dispersion around the fitted polynomial is mainly due to the sampling effect, particularly at the centre of the image where the orders are almost flat. It is worth noticing that the ELODIE orders are particularly narrow, 90% of the energy being spread over 3 pixels.
The background emission can be split into two components: a local one due to the inter-order scattering, proportional to the flux in the adjacent orders, and a diffuse one, proportional to the overall flux level on the image. Thus the level of the background contamination in each order is proportional to the flux in the order itself but also depends on the ratio between the flux in the order and the level of the overall illumination. In Fig. 10 this two-component effect is clearly visible.
In "star fibre only" exposures, the order separation is large enough to estimate the background emission from the measurement of the flux in the inter-orders. The typical error in the background measurement, using a two dimensional polynomial fit, is about 5% (see Fig. 11). Taking into account the background level (Fig. 10) we then conclude that, after subtraction, the remaining uncorrected background is lower than 0.5% of the flux in the order for the great majority of the orders.
The extraction of the orders is carried out using an optimal extraction algorithm with a cosmic-ray hit elimination based on the Horne (1986) algorithm. The spatial profile, previously measured, is used to determine the extraction zone, to compute the weight of each pixel and to detect and correct the pixels hit by cosmic rays. The extraction algorithm can be split into 9 stages:
1. The numerical extraction slit is defined as a
multiple of the ![]() of the spatial profile.
ELODIE uses a numerical slit of ± 3
of the spatial profile.
ELODIE uses a numerical slit of ± 3![]() leading
to the extraction of 99.7% of the flux spread over the orders.
leading
to the extraction of 99.7% of the flux spread over the orders.
2. A first
estimate of the extracted spectra
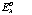 is computed:
is computed:
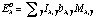 ,
where bx,y is the real fraction of the pixel to extract,
Ix,y the flux in the pixel x,y and Mx,y the mask for
the cosmic ray hits (at the beginning M=1,:x,y).
,
where bx,y is the real fraction of the pixel to extract,
Ix,y the flux in the pixel x,y and Mx,y the mask for
the cosmic ray hits (at the beginning M=1,:x,y).
3. The expected profile
px,y is computed and sampled in "real" pixels. The following
normalization is then enforced
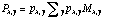
4. The variance image is computed:
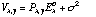 ,
where
,
where ![]() is the read-out noise of the CCD per
pixel.
is the read-out noise of the CCD per
pixel.
5. The spectrum is extracted using the optimal extraction equation of Horne:
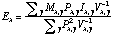
6. A Search for any cosmic ray hit is done using the Horne criterion:
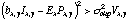 with
with ![]() clip = 4.5 and a parameter X
max to take
into account any error in the profile modelling:
clip = 4.5 and a parameter X
max to take
into account any error in the profile modelling:
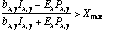
When both conditions are true, the cosmic ray is detected.
Xmax is defined for 4 parameters: (1)
![]() c
(in pixel) to describe a centering error, (2)
c
(in pixel) to describe a centering error, (2) ![]() s for
the error in the width of the spatial
profile, as a fraction of
s for
the error in the width of the spatial
profile, as a fraction of ![]() , (3)
, (3) ![]() b to take into account any uncorrected
background level, as a fraction of the amplitude of the profile and (4)
b to take into account any uncorrected
background level, as a fraction of the amplitude of the profile and (4) ![]() a to take into account any uncorrected relative
variation of pixel sensitivity. It is worth noting that without the addition
of such criteria to the "classical" Horne technique, the algorithm would not
work on high signal-to-noise spectra without using unrealistic
a to take into account any uncorrected relative
variation of pixel sensitivity. It is worth noting that without the addition
of such criteria to the "classical" Horne technique, the algorithm would not
work on high signal-to-noise spectra without using unrealistic ![]() clip values. The definition of the spatial
profile is never good enough to be used on high signal-to-noise ratio
spectra. Using a Gaussian profile, the maximal X values are computed for
each parameter:
clip values. The definition of the spatial
profile is never good enough to be used on high signal-to-noise ratio
spectra. Using a Gaussian profile, the maximal X values are computed for
each parameter:
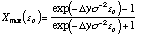
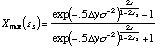
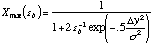
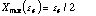
where ![]() y represents the distance (in pixels)
from the profile centre and
y represents the distance (in pixels)
from the profile centre and ![]() the standard
deviation of the Gaussian profile in pixels. In the reduction, the following
values are used:
the standard
deviation of the Gaussian profile in pixels. In the reduction, the following
values are used: ![]() c = 0.3 pixels,
c = 0.3 pixels,
![]() s = 3%,
s = 3%,
![]() b =
4% and
b =
4% and ![]() a =10%.
a =10%.
7. When the algorithm detects a cosmic ray hit at the position xi,
yj it sets
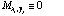 and goes back to point (2). This loop is iterated until there is no more cosmic
ray detection. The rejection scheme only permits to reject one pixel per
iteration. If more than one cosmic ray is detected during one loop, only the
pixel with the highest difference compared to the expected value is considered
as a hit.
and goes back to point (2). This loop is iterated until there is no more cosmic
ray detection. The rejection scheme only permits to reject one pixel per
iteration. If more than one cosmic ray is detected during one loop, only the
pixel with the highest difference compared to the expected value is considered
as a hit.
8. The value of hit pixels is estimated and corrected using the remaining information from the "good pixels" and the spatial profile shape.
9. The final extraction is carried out using the algorithm described in point
(5)
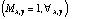
A slight mismatch between the true spatial profile and the model does not have a significant influence on the flux extracted by the weighted algorithm. A global vertical shift of about 0.2 pixels or a error of 5% in the width of the spatial profile adds a "noise" of less than 0.2% in the extracted flux (see on Fig. 12). This effect is negligible in our case. The systematic errors in the measurement of the width, the location of the orders and the maximal variation of the order positions during the night are lower than these values.
The basic format of the extracted spectra is two-dimensional images, call herein after 2-D spectra. This data structure keeps the original pixel identity along the direction of main dispersion as well as the order number. The wavelength solution is described with polynomial coefficients and stored in the image descriptors. Such a data format offers the possibility of keeping the information on the location of each spectrum bin on the CCD and therefore the original sampling.
To correct for the relative pixel sensitivity variation of the CCD, the
flat-field exposure must ideally illuminate uniformly the order profile (along
the spatial profile). Unfortunately, with a fibre-fed spectrograph, this
operation is not feasible because the width of the order is always constrained
by the fibre diameter. The standard flat-field correction for these
spectrographs is to build a flat-field spectrum and then to divide each
order of the star spectrum by the corresponding order of the flat-field
spectrum (e.g. Hall 1994). However this operation is not formally correct:
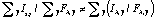 and produces a slight loss of accuracy. It is worth noticing that, if the
position and the spatial profile of the orders P remains identical during the
exposures of the star and the flat-field spectrum, then Fx,y =
Px,y Fx and
Ix,y = Px,y Ix. Therefore, the inequality becomes an equality and the
standard flat-field correction is correct. However, this condition is never
strictly met despite the high stability of the orders due to the use of
fibres.
and produces a slight loss of accuracy. It is worth noticing that, if the
position and the spatial profile of the orders P remains identical during the
exposures of the star and the flat-field spectrum, then Fx,y =
Px,y Fx and
Ix,y = Px,y Ix. Therefore, the inequality becomes an equality and the
standard flat-field correction is correct. However, this condition is never
strictly met despite the high stability of the orders due to the use of
fibres.
ELODIE is able to increase the width of the orders by moving the fibre entrance in the spectrograph. Therefore, using the tungsten lamp, we can define a true flat-field exposure. However, the illumination created by the fibre movement is not uniform along the profile (see Fig. 13). To correct this, the spatial profile of the flat-field, for every resolution bin is normalized and fitted on the extraction domain (in the Y direction) by a second order polynomial. As we expect a global and smooth variation of illumination throughout the image, the variation of the coefficients of the second-order polynomials are also
constrained by a two-dimensional polynomial :
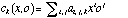 ,
where ck is the kth coefficient of the second-order polynomials, x
the X-pixel position and o the order number. Finally, the normalized
flat-field image is divided by the fitted model. In the remainder of this
paper, we will consider the flat-field image as the normalised and
corrected one.
,
where ck is the kth coefficient of the second-order polynomials, x
the X-pixel position and o the order number. Finally, the normalized
flat-field image is divided by the fitted model. In the remainder of this
paper, we will consider the flat-field image as the normalised and
corrected one.
The correction for the flat-field is split into two operations. First, the image is divided by the flat-field image to correct the relative pixel sensitivity along the spatial profile. Secondly, the 2-D spectrum is divided by the flat-field spectrum, to correct the "extracted pixel". This two-step process permits a formally correct flat-field correction and also provides the possibility of using other 2-D spectra to correct the flat-field in the X-direction (a spectro-photometric star, for example). This flexibility is important for an observational system with an automatic reduction procedure where the observer is no longer supposed to work with the raw images. Note that the use of a flat-field image is optional. If there is no flat-field image, only the "standard flat-field correction" is carried out. In particular, for spectra with S/N <300 the stability of ELODIE is so good that it is not worth using the flat-field image. The use of the standard flat-field correction, with the flat-field spectrum alone, is enough to have a good flat-field correction.
The flat-field spectrum is measured with a localization exposure and reduced in the same way as an astronomical image (offset, flat-fielded with the flat-field image - if exists-, background corrected). Every order is then fitted by a polynomial to model the blaze response and any remaining low frequency component. The flat-field spectrum is finally computed by dividing the localization spectrum by this model.
The
wavelength calibration is carried out with the thorium spectrum. The
algorithm searches, in the extracted spectrum, for a sample of unblended and
relatively strong lines selected from the atlas of Palmer & Engleman
(1983). A Gaussian is then fitted to each detected line to find its
position, and a two-dimensional polynomial is used to constrain the global
wavelength solution. Finally, the difference between the fit and the
location of the lines is computed. The lines with deviations greater than
2.75 times the r.m.s. are rejected. This last step is iterated until there
is no more rejection. Usually the convergence occurs after about 10 steps
and 10% of the lines of the initial sample are rejected. The polynomial used
is an expansion of the grating equation for small deviation angles:
m![]() = P(x,m), where m is the order number and x the
pixel position along the direction of the main dispersion. The quality of
the calibration is finally checked by cross-correlating the calibrated
spectrum with a thorium template built from the atlas. Every thorium lamp
exposure produces a new wavelength calibration which is valid until the
exposure of the next one.
= P(x,m), where m is the order number and x the
pixel position along the direction of the main dispersion. The quality of
the calibration is finally checked by cross-correlating the calibrated
spectrum with a thorium template built from the atlas. Every thorium lamp
exposure produces a new wavelength calibration which is valid until the
exposure of the next one.
The degree of the polynomial is 3 and 5 respectively for the x and m space. The final solution uses typically 1100 lines and the r.m.s. between the fit and the location of the lines is always around 0.002Å (about 120 m s-1).
To estimate the accuracy of the wavelength calibration, we have
computed the cross-correlation function of each order alone for 15 thorium
spectra measured over two nights. Within each order, the thorium spectrum
has only about 30 lines usable for the cross-correlation. Therefore their
radial velocity is not strictly zero because of line mismatching and
sampling effects. Nevertheless, the velocity offset of each order must be
the same for all the thorium spectra and the velocity dispersion around this
value gives the typical wavelength calibration uncertainty for each order.
We measure about 20 m s-1 (see Fig. 14) typical accuracy per
order and estimate the global uncertainty in the radial velocity due to the
wavelength calibration alone at about 3 m s-1
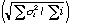 .
.
The computation algorithm for the cross-correlation function (CCF) is very much like the optical cross-correlation process used by CORAVEL (Baranne et al. 1979, Queloz 1995b). The template spectrum is composed of box-shaped emission lines of equal amplitude and plays the role of the real spatial filter of the CORAVEL mask.
The CCF is computed from a wavelength calibrated 2-D spectrum. For stellar spectra, only the orders having an average signal-to-noise (S/N) ratio greater than 0.15 are used. Monte-Carlo simulations have shown that below this value the orders add noise to the CCF. The value of the Earth barycentric velocity towards the star is taken into account to constrain the wavelength domain of each order so as to keep the wavelength range used in the CCF calculation independent of the period of measurement. From the wavelength limits of each order and the velocity range to compute, the algorithm selects, for each order, the lines which will always be in the wavelength domain during the scan. The CCF C(v) is computed step by step for each velocity point without either rebinning or merging the orders:
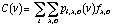
where fx,o is the value of the 2-D spectrum for the order o at the pixel location x and pl,x,o is the fraction of the lth line of the template which falls into the pixel (x,o) at the velocity v. The CCF is then normalized and brought to the solar system barycentric reference frame using the algorithm of Stumpff (1980). Finally, a Gaussian, or a double Gaussian in case of SB2 spectra, can be fit by the observer.
A systematic study have been carried out in order to avoid any error in the correction of the Earth's motion due to the algorithm itself. In particular we have compared the results from the Stumpff algorithm with those from the Bretagnon & Francou (1988) algorithm and also with those from a third independent program kindly provided by F. Chollet (private communication). In all cases the velocity difference was below 1 m s-1.
Two standard templates or masks are available. They have been built following the Baranne et al. (1979) technique, using Bell & Gustafsson synthetic spectra of an F0V and K0III star.
Many Monte-Carlo simulations with ELODIE spectra were carried out to investigate the error in the parameters of the CCF fitted by Gaussians due to photon noise and CCD read-out noise. With the help of the equation (10) of Queloz (1995b) a similar expression has been computed and calibrated specifically for ELODIE. The uncertainty in the radial velocity and the width of the CCF due to the photon noise is:
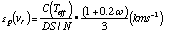
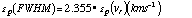
where C(Teff) is a constant which depends on the spectral type of the star
and on the mask used, ![]() the (noiseless) FWHM
(in km s-1) of the CCF, D its (noiseless) relative depth and S/N
the mean signal-to-noise ratio. The C(Teff) parameter has been computed from
Monte-Carlo simulations for both standard masks using ELODIE spectra of G, K
and M dwarfs (Table 2). The parameter C(Teff)/D is inversely proportional to
the relative efficiency of each mask. It is clear from Table 2 that the best
efficiency is reached when the spectrum is matched by the template (F mask
for a F star, etc.).
the (noiseless) FWHM
(in km s-1) of the CCF, D its (noiseless) relative depth and S/N
the mean signal-to-noise ratio. The C(Teff) parameter has been computed from
Monte-Carlo simulations for both standard masks using ELODIE spectra of G, K
and M dwarfs (Table 2). The parameter C(Teff)/D is inversely proportional to
the relative efficiency of each mask. It is clear from Table 2 that the best
efficiency is reached when the spectrum is matched by the template (F mask
for a F star, etc.).
Table 2.
Value of the C(Teff) constant of Equ. (9). The C(Teff)/D
parameter is a inverse measurement of the mask efficiency.
--------------------------------------------------------
star Teff C(Teff) C(Teff)/D
F mask K mask F mask K mask
--------------------------------------------------------
4000 0.09 0.050 0.45 0.29
5000 0.08 0.040 0.30 0.27
6000 0.07 0.045 0.29 0.37
--------------------------------------------------------
In the case of a "star fibre and sky fibre" exposure, the CCF of the star is automatically corrected for the sky CCF (due to the moon light). The sky CCF is computed using the same wavelength limits and the same template spectrum as for the star CCF. If a Gaussian can be reasonably fitted to the sky CCF, the fit is subtracted from the CCF of the star (see Fig. 15); otherwise, only the mean level of the sky-CCF is used.
We measure, with the thorium emission lines, a sampling per resolution element (FWHM) of 2.25 ± 0.2 (pixels) in the blue and 2.1 ± 0.2 (pixels) in the red. After wavelength calibration, the resolution of the lines (FWHM) is 7.4 km s-1 in the blue and 7.0 km s-1 in the red corresponding to an average resolution power of 42000. Figure 16 displays a part of the ELODIE spectrum of the G0V star HD109358.
During good quality nights, in one hour exposure time, a S/N of 100
per pixel at ![]() = 5600 Å can be
achieved for a star of mV=9.75. This corresponds to a global transmission of
1.3%. Taking into account 60% transmission for the atmosphere and the
telescope, 65% for the CCD and 1.5" seeing, this corresponds to 4.2%
efficiency for ELODIE alone.
= 5600 Å can be
achieved for a star of mV=9.75. This corresponds to a global transmission of
1.3%. Taking into account 60% transmission for the atmosphere and the
telescope, 65% for the CCD and 1.5" seeing, this corresponds to 4.2%
efficiency for ELODIE alone.
The relative sensitivity of ELODIE displayed in Fig. 17 indicates a severe loss of efficiency in the blue part of the spectrum. This effect is partly due to the CCD response but is, in our case, strengthened by the blaze response of the grism, which has its maximum efficiency at 5500 Å and therefore has a poor performance in the blue domain.
The evaluation of the spectroscopic quality of ELODIE spectra was
made by comparison of the observed equivalent widths in the solar spectrum
with the values of the Moore (1966) atlas. Using a spectrum of a minor
planet (Vesta) and a set of 221 isolated lines, the following regression was
measured: W![]() (Moore) = 0.975 W
(Moore) = 0.975 W![]() (ELODIE) +0.6 (mÅ) (see Fig. 18). The
small value of the zero point (0.6 mÅ) indicates that only a little
background contamination remains in this spectrum. The slope is not equal to
unity, but a similar result is obtained for the MUSICOS echelle
spectrograph (Baudrand & Böme 1992) in spite of the use of a more
sophisticated background modelling.
(ELODIE) +0.6 (mÅ) (see Fig. 18). The
small value of the zero point (0.6 mÅ) indicates that only a little
background contamination remains in this spectrum. The slope is not equal to
unity, but a similar result is obtained for the MUSICOS echelle
spectrograph (Baudrand & Böme 1992) in spite of the use of a more
sophisticated background modelling.
The stability of the spectrograph in wavelength during the night
depends on many parameters. The strongest variability (![]() Vr ~ 300 m s-1) occurs during the
filling of the dewar, but after 45 minutes, the effects of this strong
thermal shock vanish. During the night, ELODIE is little dependent on the
temperature because its thermal inertia is high enough and also because the
spectrograph room is thermostated. The main remaining influence is the
atmospheric pressure that changes the air refractive index and shifts the
zero of the calibration (100 m s-1 mmHg-1). There is
also a small flexure effect due to the dewar unloading which moves the
orders in the direction perpendicular to the main dispersion. The orders are
vertically shifted by about 0.1 pixels during the night and the effect seen
on the wavelength calibration is about 50 m s-1.
Vr ~ 300 m s-1) occurs during the
filling of the dewar, but after 45 minutes, the effects of this strong
thermal shock vanish. During the night, ELODIE is little dependent on the
temperature because its thermal inertia is high enough and also because the
spectrograph room is thermostated. The main remaining influence is the
atmospheric pressure that changes the air refractive index and shifts the
zero of the calibration (100 m s-1 mmHg-1). There is
also a small flexure effect due to the dewar unloading which moves the
orders in the direction perpendicular to the main dispersion. The orders are
vertically shifted by about 0.1 pixels during the night and the effect seen
on the wavelength calibration is about 50 m s-1.
A monitoring of the wavelength variation is compulsory to achieve radial velocity measurements with an accuracy better than 50 m s-1. Such measurements are done using the sky-hole illuminated by the thorium lamp during stellar exposures. The wavelength solutions of each optical path (star and sky) are independent, but series of tests have shown that their variations are strongly correlated. Therefore, the sky-way can be used to monitor the wavelength calibration shift of the star-way.
During 2 nights, 40 thorium exposures were carried out. In order to
simulate the worst experimental situation, we also made a serie of thermal
shocks in the spectrograph room (![]() T~1°).
Under such conditions, the velocity variations due to the calibration shift
between 2 successive exposures sometimes reached 150 m s-1.
However, despite the strong variability of the spectrograph during this
experiment, we observe that the velocity variations between both optical
paths (star and sky) are very small. Using the first exposure of the series
as a wavelength calibration for each way, the velocity differences between
the ways, for each successive exposure, exhibit only a 2.5 m s-1
standard deviation (see Fig. 19). Note that a small velocity correction is
taken into account to correct a slight mismatch between the two optical
paths. Finally, by adding the uncertainty in the wavelength calibration of
the first exposure, we conclude that ELODIE is able to provide an accuracy
of about 4 m s-1 with this technique.
T~1°).
Under such conditions, the velocity variations due to the calibration shift
between 2 successive exposures sometimes reached 150 m s-1.
However, despite the strong variability of the spectrograph during this
experiment, we observe that the velocity variations between both optical
paths (star and sky) are very small. Using the first exposure of the series
as a wavelength calibration for each way, the velocity differences between
the ways, for each successive exposure, exhibit only a 2.5 m s-1
standard deviation (see Fig. 19). Note that a small velocity correction is
taken into account to correct a slight mismatch between the two optical
paths. Finally, by adding the uncertainty in the wavelength calibration of
the first exposure, we conclude that ELODIE is able to provide an accuracy
of about 4 m s-1 with this technique.
The investigation of the short-term radial velocity measurement accuracy has been carried out with the bright star HD109358 (G0V). Successively, during 3 hours, 13 stellar exposures (simultaneous thorium type), of 7 minutes each, were obtained. The individual velocities show a standard deviation of 6 ± 1 m s-1. As the signal-to-noise ratio of each spectrum is high enough (S/N > 150) to neglect the photon-noise errors, this corresponds to the short-term radial velocity instrumental uncertainty of ELODIE. However, to search for planets or brown dwarfs by Doppler shift, the individual radial velocity accuracy over the long term is a more crucial parameter. Ideally, the long term accuracy should be close to the short term accuracy, but this is usually not the case because of long term instabilities of the spectrograph and of the shift of the lines of the star over the detector during the year.
To measure accurately and with objectivity the value of the long
term radial velocity accuracy of ELODIE, we have used all the radial
velocities measured since April 1994 as a part of the sub-stellar companion
search program (Mayor et al. 1996). For a set of stars with constant
velocities, we expect the P(![]() 2)
distribution to be flat. Thus, the value of the instrumental error can be
tuned up to meet this statistical property (Duquennoy et al. 1991b). Using
106 stars of the sample, measured at least twice, we find, using this
technique, an instrumental uncertainty of 13 m s-1. This result
is excellent by comparison with the performances achieved by other groups
(see Kürster et al. 1994).
2)
distribution to be flat. Thus, the value of the instrumental error can be
tuned up to meet this statistical property (Duquennoy et al. 1991b). Using
106 stars of the sample, measured at least twice, we find, using this
technique, an instrumental uncertainty of 13 m s-1. This result
is excellent by comparison with the performances achieved by other groups
(see Kürster et al. 1994).
The instrumental long term radial velocity uncertainty is
significatively larger than the short term accuracy. However, note that for
ELODIE a velocity shift of 12 m s-1, at CCD scale, corresponds to
1/300 of the pixel size. Jorden et al. (1994) show that at this scale the
CCD is strongly non-uniform and each pixel has an intrinsic uncertainty on
its true centre of gravity. Considering 4000 lines spread over 5 pixels and
an uncertainty of 1/4 pixel in the location of each pixel, with simple
statistics, we find an error in the average location of
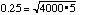 =1/600
pixel corresponding to 6 m s-1. The addition of this uncertainty to
the short term accuracy computed above shows that a part of the long term
accuracy is certainly due to this effect. The use of a CCD with smaller size
pixels could be an easy way to improve the long term accuracy.
=1/600
pixel corresponding to 6 m s-1. The addition of this uncertainty to
the short term accuracy computed above shows that a part of the long term
accuracy is certainly due to this effect. The use of a CCD with smaller size
pixels could be an easy way to improve the long term accuracy.
Table 3.
Summary of the ELODIE instrumental characteristics
------------------------------------------------------------------------------------------
Instrumental parameter Measured value
Typical resolution power 42 000
Pixel sampling per FWHM 1.9-2.45
Usable wavelength domain (blaze response > 50%) 3906-6811 Å
Number of orders 67
Typical vertical width of the orders (90% of the energy) 3 pixels
CCD read-out noise 8.5 e-
Overall transmission at 5600 Å (maximum of the blaze) 1.3%
Internal precison of the wavelength calibration 3 m /s (20 m /s per order)
Observed instrumental velocity error 13 m /s (long term)
-------------------------------------------------------------------------------------------
We have described
ELODIE, the new spectrograph of the Haute-Provence Observatory, a fibre-fed
echelle spectrograph with a fixed optical system, designed to provide
accurate radial velocity measurements. The main dispersion is done by ![]() = 4 echelle-grating and the cross-dispersion by
the combination of a prism and a grism. This special optical mounting
allows us to record in one single exposure a wavelength domain ranging from
3906 Å to 6811Å with a resolution of 42000 on a relatively small
CCD (1024x1024). An automatic data reduction program, integrated into the
spectrograph data flow, reduces all images directly after the exposure. The
software also includes the computation of cross-correlation functions. This
very original ability proves to be very useful to interact rapidly with the
observations (in particularly for the search for small velocity
variations). It also saves the observer the labour of reducing echelle
spectra. A summary of the instrumental characteristics of ELODIE is
presented in Table 3.
= 4 echelle-grating and the cross-dispersion by
the combination of a prism and a grism. This special optical mounting
allows us to record in one single exposure a wavelength domain ranging from
3906 Å to 6811Å with a resolution of 42000 on a relatively small
CCD (1024x1024). An automatic data reduction program, integrated into the
spectrograph data flow, reduces all images directly after the exposure. The
software also includes the computation of cross-correlation functions. This
very original ability proves to be very useful to interact rapidly with the
observations (in particularly for the search for small velocity
variations). It also saves the observer the labour of reducing echelle
spectra. A summary of the instrumental characteristics of ELODIE is
presented in Table 3.
The efficiency of ELODIE allows us to observe stars of 9th-magnitude class for spectroscopic works. During good nights, observations of 16th-magnitude stars are also possible to measure for example the radial velocity at 1 km s-1 precision by cross-correlation. We clearly see that the potential research field of this instrument is very wide, e.g.: stellar atmosphere physics (pulsating stars, abundances studies), Galactic studies (velocity, metallicity, Teff), study of clusters, pre-MS stars (membership, binarity, rotation) and binary star studies.
The long term radial velocity instrumental uncertainty of ELODIE is 13 m s-1. This indicates that our technique of simultaneously monitoring the spectrograph by using a second fibre, illuminated by a thorium-argon lamp, is able to provide similar performances to that of absorption cell instruments. With its wide wavelength range and its relatively good transmission, ELODIE can measure the velocity of a solar type star of 9th magnitude, with 5 m s-1 photon error, in less than 30 minutes. It is then possible to monitor a large number of stars, using a reasonable amount of telescope time. ELODIE is a suitable instrument for hunting Jupiter size planet around nearby stars.
A copy of this spectrograph called CORALIE will be installed at La Silla (ESO, Chili) on the new 1.20-meter telescope of the Geneva Observatory. CORALIE is almost identical to ELODIE. However, the smaller focal length of this telescope, compared to the 193cm of the OHP, will increase the resolution up to 50000. The detector is also different. It has smaller pixels and will provide a better sampling (3 instead of 2 pixels per resolution element). We expect that all these modifications will improve the accuracy of the radial velocities.
acknowledgements We are extremely grateful to the region
"Provence Alpes Côtes d'Azur" (PACA) for its continuous support of
this project. In particular, the design of the instrument was only possible
thanks to grants offered by this region. The two spectrographs of this
project have been financed by the PACA, the INSU (France), the University of
Geneva and by the FNRS (Switzerland). We are thankful to these organizations
for their confidence and generous support. We have benefited from the
invaluable help of many colleagues. We present our particular
acknowledgements to Catherine Grezes-Besset of the Ecole de Physique de
Marseille, for having developed the filter located in front of the CCD. We
also thank Luc Weber of the Geneva Observatory for providing us with
important items of software and for his continuous and enthusiastic
support. We are also grateful to Raphael Cautain for his contribution to the
data reduction software, to Denis Gillet and F. Chollet for their
contribution to tests and improvement of the algorithm of the Earth velocity
correction, to Frédéric Pont for his careful reading of the
manuscript and to John Hearnshaw, our referee, for his comments and
suggestions. We finally thank Philippe Véron, former director of the
OHP, for his strong support along all the critical phases of this project.
Fig. 2. ELODIE echelle spectrum of a hot star recorded on the CCD Tk1024. 67 orders are usable, starting with the 156th order and ending with the 90th (ranging from 3906Å to 6811Å). Note that the orders are clearly separated and that the inter-order spacing is remarkably constant over the whole wavelength range.
Fig. 3. ELODIE spot-diagrams.
Fig. 4. Optical layout of the calibration system in the front end adaptor: 1. tungsten lamp and diffuser, 2. hollow cathode thorium lamp, 3. colour corrector filter. 4. static beam-splitter, 5. relay achromat, 6. mirrors for beam angular splitting, 7. removal mirror and beam splitting (part of the accelerometry experiment), 8. optical fibre of the Fabry-Perot light (part of the accelerometry experiment), 9. circular wedge 10. pupil, 11 achromat (to put the pupil at infinity), 12. calibration mirror, 13. fibre mask, 14. concave mirror with 2 holes, 15. spectrometer linking fibres and aperture converter, 16. aperture converter optics and rhomboid prisms (to bring the beams closer to the focus of the collimator).
Fig. 5. Transmission of the fibres for various output apertures. The
entrance beam has a fixed aperture of f/4.5. The dotted lines represent the
incoming flux. The filled and empty dots indicate the flux coming out at
respectively ![]() =5461 Å and
=5461 Å and ![]() = 4047 Å
= 4047 Å
Fig. 6. Small part of the raw image for the three different types of stellar exposure available. a "star fibre only", b star fibre and sky fibre simultaneously illuminated (here by the tungsten lamp), c "simultaneous thorium": star on the star hole and the sky hole simultaneously illuminated by the thorium lamp.
Fig. 7. Display of the location of the orders found by the program (white points), in the four corners of the image: a top left, b top right, c bottom left, d bottom right. Note that the display of the position of the orders is here sampled by the CCD. Obviously the position is known to a better accuracy than the pixel size.
Fig. 8. Profiles of the orders for a localization image (black squares) compared to the fitted Gaussian shape for various positions on the image. The profiles from a to c correspond to the 152nd order for the X-position 79,487 and 946 respectively. The profiles d to f are for the 124th order and g to i for the 94th order.
Fig. 9. ![]() i,j measured by the fit of a set of elongated
two-dimensional Gaussians (points): left for X=640 along all the orders.
Right for the central order (124th) along the direction of the main
dispersion. The lines are the fitted polynomials
i,j measured by the fit of a set of elongated
two-dimensional Gaussians (points): left for X=640 along all the orders.
Right for the central order (124th) along the direction of the main
dispersion. The lines are the fitted polynomials ![]() (x,o). The noise
around the fitted function is mainly due to the sampling noise.
(x,o). The noise
around the fitted function is mainly due to the sampling noise.
Fig. 10. a S/N distribution across the orders for a tungsten spectrum at the location X=500 (solid line) and X=200 (dotted line). b the flux ratio (in percent) between the tungsten spectrum and the inter-order "spectrum" (or background "spectrum"). In the red part, the background level is proportional to the flux in the order which is a characteristic of a local background contamination. The rise of the relative background level in the blue part of the spectrum, mirror image of the flux distribution, is a feature of a high contamination by the diffuse component.
Fig. 11. Top Cross orders tracing at X=500 of a localization exposure
superimposed with the polynomial fit of the background. We notice around Y=500
a little bump due to the contamination by some uncorrected blue wavelength
coming from the second order of the cross-disperser. Bottom Difference
between the fit and the background level ![]() f/f=(fimage-ffit)/ffit. The
typical error in the background measurements is below 5%.
f/f=(fimage-ffit)/ffit. The
typical error in the background measurements is below 5%.
Fig. 12. Simulation of the variation of the extracted flux for various
simulated mismatches between the model and the true geometry for the 117th
order (![]() f/f=(ftrue-fmismatch)/ftrue). Upper figure the order
are vertically shifted of 0.2 pixels. Lower figure the width of the
spatial profile is increase by 5%.
f/f=(ftrue-fmismatch)/ftrue). Upper figure the order
are vertically shifted of 0.2 pixels. Lower figure the width of the
spatial profile is increase by 5%.
Fig. 13. Top Cross orders tracing at X=500 of a flat-field exposure, superimposed with a localization exposure for comparison. Bottom displays the same crosscut of a flat-field image (corrected from the non-uniform illumination and normalized).
Fig. 14. Dispersion of the radial velocity in each order of a thorium spectrum, computed with 15 spectra measured over 2 days. Across most of the spectrum the typical accuracy per order is about 20 m s-1.
Fig. 15. a: CCF of a faint star contaminated by the CCF of the solar spectrum (indicated by an arrow). b: Same CCF after the subtraction of the CCF of the sky. The line is the Gaussian fit.
Fig. 16. Part of the spectrum of the G0V star HD109358 (centre of the 117th order.
Fig. 17. Relative efficiency of ELODIE to 5600 Å, over the whole wavelength range, computed from the observation of the spectro-photometric OV star HD93521. The squares represents the relative quantum efficiency of the CCD.
Fig. 18. Comparison between the ELODIE equivalent widths and the Moore
(1966) results for the solar spectrum. The line represents W![]() (Moore) =
W
(Moore) =
W![]() (ELODIE).
(ELODIE).
Fig. 19. a Histogram of the velocity shifts between the two way (sky
fibre - star fibre). The line is a Gaussian with ![]() =2.3 m
s-1. Note that a correction is done to suppress a slight mismatch
between the two optical paths:
=2.3 m
s-1. Note that a correction is done to suppress a slight mismatch
between the two optical paths: ![]() Vr(sky) =
Vr(sky) =
![]() Vr(star)-.04\
Vr(star)-.04\![]() Vr(star)+0.6 (
Vr(star)+0.6 (![]() Vr is the velocity
variation of the spectrograph in units of m s-1). b histogram
of the variation of the spectrograph monitor by the star-way during the
measurements.
Vr is the velocity
variation of the spectrograph in units of m s-1). b histogram
of the variation of the spectrograph monitor by the star-way during the
measurements.