

Next: Phasing a hierarchy of
Up: A hierarchical phasing algorithm
Previous: Introduction
We considered the case of densified-pupil interferometers ([Labeyrie 1996]), a
new class of instruments where beams are combined like in Michelson's
20- and 50-feet systems, but with more than 2 beams. The
densified-pupil concept evades the ``golden rule'', once thought inescapable,
which stated that imaging interferometers had to be
Fizeau-like ([Labeyrie 1983,Traub 1986,Beckers 1986]). Fizeau-type interferometers
having many apertures can produce snapshot images, but not if the
aperture is highly diluted since most energy then goes in the numerous
side-lobes rather than in the central interference peak. Densifying the
exit pupil (Fig. 1), by extending to many apertures the kind
of ``periscopic'' arrangement originally used by Michelson, can
concentrate the energy in the interference peak, but appeared to destroy
the isoplanaticity needed to observe resolved objects.
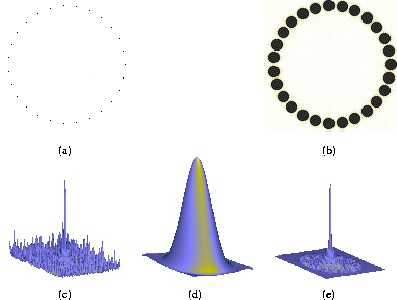
Figure 1:
Image formation with a densified-pupil array. The array's exit
pupil is the convolution of an array of Dirac peaks a-, with a sub-pupil.
The Fourier transform of the peak array c-, called the interference
function, here has a central peak surrounded by 54 lower peaks. The
broad multiplicative envelope, called the diffraction function, shown in
d- is the Fourier transform of the sub-pupil, made proportionally
larger in the exit pupil than in the entrance aperture. The image of a
non-resolved star is obtained in e- as the product of the patterns c-
and d-. With a resolved star, only the interference function is becoming
convolved with the star function if the pupil is highly
densified.
 |
The solution recently found uses a restricted class of Michelson-type
arrangements where:
- the pattern of sub-aperture centres is identical in the entrance and
the exit pupils.
- all sub-pupils are of homogeneous size and shape.
It can provide full energy concentration in the combined high-resolution
image, but the field and object size are restricted to about 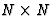 resolved elements, if N is the number of apertures.
resolved elements, if N is the number of apertures.
If the exit pupil is highly densified, as is necessarily the case
in large space instruments such as the proposed Exo-Earth
Discoverer ([Boccaletti et al. 1999]), the Terrestrial Planet Finder ([Angel & Woolf 1997,Woolf 1997])
and the Exo-Earth Imager ([Labeyrie 1998]), then a valid approximation for
the monochromatic intensity distribution B(x, y), in the combined focal
image was shown to be ([Labeyrie 1996]):
| ![\begin{displaymath}
B_{(x,y)} \approx {\gamma_{d}}^{-2} A_{(x,y)} \left
[O_{(\frac{x}{\gamma_d}, \frac{y}{\gamma_d})}\otimes I_{(x, y)}
\right],\end{displaymath}](img3.gif) |
(1) |
where O(x,y) is the intensity distribution of the object. I(x,y)
is the interference function of the interferometer, i.e. the Fourier
transform of an array of Dirac peaks located at the sub-aperture centres,
A(x, y) the diffraction pattern from one sub-aperture and
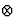 is the convolution symbol. Finally, x and y are the
coordinates in the focal plane.
The quantity
is the convolution symbol. Finally, x and y are the
coordinates in the focal plane.
The quantity 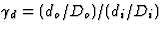 describes the amount
of pupil densification, Di and di, being the pupil and sub-pupil
sizes at the entrance, while Do and do are the corresponding
quantities at the exit pupil.
describes the amount
of pupil densification, Di and di, being the pupil and sub-pupil
sizes at the entrance, while Do and do are the corresponding
quantities at the exit pupil.
Eq. 1 shows that the interference function I(x,y)
(Fig 1.c) is convolved with the object's intensity distribution and
then multiplied by the wide diffraction pattern of the sub-pupil
(Fig. 1.d). For the large values of the pupil densification this
latter pattern is considered insensitive to object position and simply
behaves, where Eq. 1 is valid, as a windowing
function which multiplies the convolution.
I(x,y) generally has a central peak if the sub apertures are phased, a
desirable situation which improves greatly the quality of the snapshot
image B(x,y) (without phasing, speckle interferometry can still
produce images). In monochromatic light, the phasing is required modulo
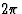 radians, but reaching the phasing condition at numerous
wavelengths simultaneously requires all optical paths to be equal, as is the
case for a perfect giant telescope. In our simulation we used 3
wavelengths to reduce the path differences from
radians, but reaching the phasing condition at numerous
wavelengths simultaneously requires all optical paths to be equal, as is the
case for a perfect giant telescope. In our simulation we used 3
wavelengths to reduce the path differences from 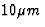 to nearly
zero. The example discussed here involves 27 identical apertures, arrayed
along a circle, but the algorithm can be extended to any hierarchy of
triplets arbitrarily arrayed.
to nearly
zero. The example discussed here involves 27 identical apertures, arrayed
along a circle, but the algorithm can be extended to any hierarchy of
triplets arbitrarily arrayed.


Next: Phasing a hierarchy of
Up: A hierarchical phasing algorithm
Previous: Introduction
Ettore Pedretti
4/20/1999
![]() radians, but reaching the phasing condition at numerous
wavelengths simultaneously requires all optical paths to be equal, as is the
case for a perfect giant telescope. In our simulation we used 3
wavelengths to reduce the path differences from
radians, but reaching the phasing condition at numerous
wavelengths simultaneously requires all optical paths to be equal, as is the
case for a perfect giant telescope. In our simulation we used 3
wavelengths to reduce the path differences from ![]() to nearly
zero. The example discussed here involves 27 identical apertures, arrayed
along a circle, but the algorithm can be extended to any hierarchy of
triplets arbitrarily arrayed.
to nearly
zero. The example discussed here involves 27 identical apertures, arrayed
along a circle, but the algorithm can be extended to any hierarchy of
triplets arbitrarily arrayed.