Mean flux adjustment

The fluxes of the target and reference stars being usually very different, one has to put them on a common scale. It was decided to move the reference spectrum to the mean level of the object spectrum. The first idea, based on theoretical considerations, was to solve this problem by weighted least-squares, finding u such that:

$$S_k={1 \over n_k-1}\sum_{i\in E_k} \Biggl[{F_{obj}(i,k)-u_k F_{ref}(i,k)\over \sigma_{i,k}}\Biggr]^2$$

where:
F_obj(i,k) is the flux of the target star at pixel i and order k. F_ref(i,k) is the interpolated flux of a reference star interpolated at the same intrinsic wavelength, as explained in Sect. 4.1. E_k is the set of pixels of order k, for which none of the F_obj(i,k) or F_ref(i,k) are flagged at - 100.0 value. n_k is the number of elements in E_k, typically 800 for a single order and $\sigma_{i,k}$ is the combined noise affecting the numerator flux difference.

Thence S_k is nothing else than the reduced $\chi^2$ of the fit. In the particular case in which a perfect twin of the target star exists in the library (no intrinsic difference, impact of noise only) the expected value of $\chi^2$ is 1, with a variance of 2/(n-1). It is of course advantageous to combine the $\chi^2$ of several orders, because this is equivalent to increase n, and to decrease the noise $\sqrt{2/(n-1)}$.For example, with 10 orders, an intrinsic rms difference of only 1.5 per cent can, theoretically, be detected with an observational S/N of 10. The implementation needs some iterations, because the noise on the numerator depends upon u, not known at the beginning.

However, after many tests, described in the following section, it was found that good results could be obtained with a simpler equivalent technique. Instead of weighting the terms in the expression of S_k by $({1 \over \sigma_{i,k}})^2$,we chose to weight them by the response curve B_k (see Sect. 3.2) which is proportional to ${1 \over \sigma^2}$ when the photon noise dominates, which is the case at S/N > 10. The least square adjustment may then be replaced by finding the value u_k for each order, which minimizes the expression :

$$S^{'}_k= {1 \over n_k-1}\sum_{i \in E_k} (F_{obj}(i,k)-u_k F_{ref}(i,k))^2 B_k(i)$$

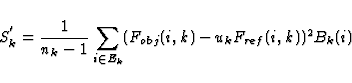
giving lower weight to the edges of the order, in the right proportion. This leads to a simple formula to determine u:

$$u_k = { \sum_{i \in E_k} F_{obj}(i,k) F_{ref}(i,k) B_k(i) \over \sum_{i \in E_k} F_{ref}^2(i,k) B_k(i)}$$

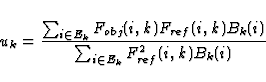
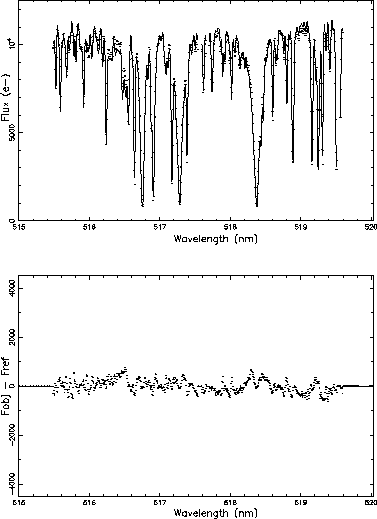
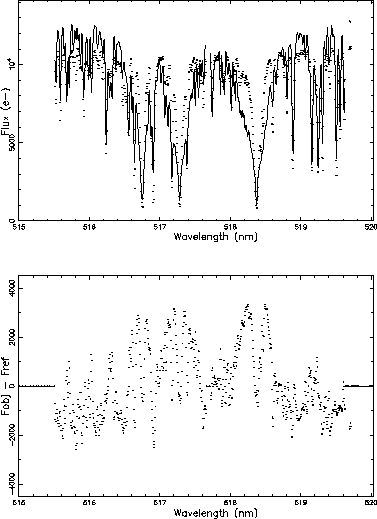
Then, the variance is calculated for each order. Figure 4 shows the fit between HD 41597 and HD 40460 (stars with similar parameters) and Figure 5 shows the fit between HD 41597 and HD 4628 (stars with different parameters).

  

Figure: The upper part of the figure shows the fit between HD 41597, in points, taken as the target ($T_\mathrm{eff}$ = 4700 K, $\log g$ = 2.38, [Fe/H] = -0.54) and HD 40460 taken as the reference star ($T_\mathrm{eff}$ = 4741 K, $\log g$ = 2.00, [Fe/H] = -0.50). The lower part shows the difference between their fluxes.

  

Figure: The upper part of the figure shows the fit between HD 41597, in points, taken as the target ($T_\mathrm{eff}$ = 4700 K, $\log g$ = 2.38, [Fe/H] = -0.54) and HD 4628 taken as the reference star ($T_\mathrm{eff}$ = 4960 K, $\log g$ = 4.60, [Fe/H] = -0.29). The lower part shows the difference between their fluxes.

Now comes the question of properly combining the information contained in the different orders. This is not a trivial question. First, there is a large variation of the S/N from the blue to the red orders. Second the spectral information contained in each order is unequal.

The first problem is solved by weighting the variance obtained on each order by the the inverse of its mean flux. The degree of ressemblance between the target and the reference star is characterized by the expression :

$$S_k = {1 \over N-n_b}\sum_{k \in K} {(n_k - 1)S^{'}_k \over <F_k\gt}$$

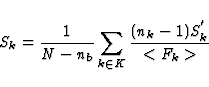
with :

$$N = \sum_{k \in K} n_k$$

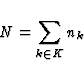
where :
K is the set of orders kept in the final result(see the next paragraph), n_b the number of orders contained in K and <F_k> the mean flux of the target star for each order. This expression is in practice equivalent to a reduced $\chi^2$.

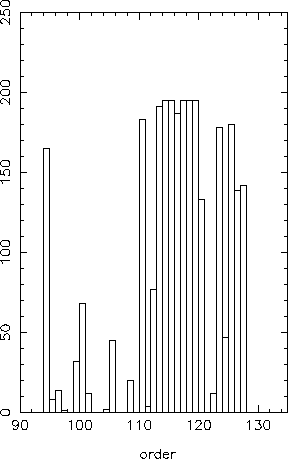
The second problem is the fact that some orders include strong lines of various elements, whereas some others are almost free of lines. For example, order 119 including the Mg I triplet appears to be one of the most significant orders for every star. Orders 94 and 127 containing $H_{\alpha}$ and $H_{\beta}$ are very useful for effective temperature determinations. Howewer its worth noticing that all orders depend on the three parameters, which can not be estimated independently. The relative relevance of the different orders has been studied. In order to select the best orders for each target. The rms deviation of the fluxes, with respect to the mean flux, caused by spectral lines plus noise, is computed. The 15 orders for which the ratio of this global modulation to pure noise modulation is the highest, are kept. This set of orders changes from one target star to another, but the orders 127, 119 and 94 (including respectively $H_{\beta}$,the Mg I triplet and $H_{\alpha}$) are selected in almost every set. The number of 15 has been chosen after a number of ``try and see'' experiments over various S/N. A larger number of orders introduce noise instead of information. Figure 6 shows the relative relevance of each order.

  

Figure: Relative relevance of each order. The test has been performed by comparing each reference star to the others ($\sim$ 40000 comparisons), by keeping for each comparison the 15 orders which give the highest rms and by counting the occurences of each order in this list.

For a given target star, the comparison is performed with the 211 reference stars of the library.

The 10 reference stars showing the lowest reduced $\chi^2$ are selected. The solution is given by the weighted mean of the parameters of the reference stars whose reduced $\chi^2$ is lower than 1.11 times the lowest one. The upper limit of $11\%$ has been empirically defined during the phase of test (see Sect. 6) and is valuable only for target stars with $S/N \geq 30$. For smaller S/N the limit is decreasing (i.e. $1\%$ for S/N = 10).

  

Figure: Distribution of the 211 reference dwarfs, sub-giants and giants in the plane ($T_\mathrm{eff}$, [Fe/H]). Dots represent dwarfs ($\log g \geq 4.2$), asterisks represent turn-off stars ($4.2 \gt \log g \geq 3.7$), open circles represent giants ($\log g < 3.7$)and the Sun is represented by its usual symbol. The figure is divided in four zones (from A to D) refered to in Sect. 6.