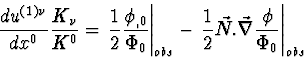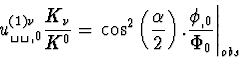


Next: La scintillation.
Up: La scintillation.
Previous: Le terme spectral intégré.
Il reste à évaluer la perturbation 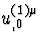 de la quadrivitesse
de l'observateur au passage d'une onde scalaire, pour un observateur en chute
libre, i.e dont la trajectoire est une géodésique de la métrique
de la quadrivitesse
de l'observateur au passage d'une onde scalaire, pour un observateur en chute
libre, i.e dont la trajectoire est une géodésique de la métrique
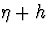 qui s'écrit
qui s'écrit
| 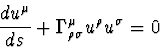 |
(78) |
avec par définition
| 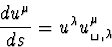 |
(79) |
ce qui donne au premier ordre, compte tenu de u(0)=(1,0,0,0)
| 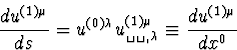 |
(80) |
Comme 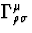 est du premier ordre en h d'après (B.3)
et (B.11), la
linéarisation de (C.49) donne avec (C.51), en se plaçant dans la
jauge des coordonnées harmoniques qui permet d'éliminer d'après (B.18)
les composantes h0 iE
est du premier ordre en h d'après (B.3)
et (B.11), la
linéarisation de (C.49) donne avec (C.51), en se plaçant dans la
jauge des coordonnées harmoniques qui permet d'éliminer d'après (B.18)
les composantes h0 iE
Il s'ensuit que
| 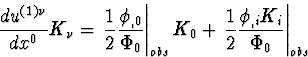 |
(81) |
En notant Ni les composantes spatiales du vecteur unitaire 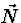 donnant la direction de propagation des rayons lumineux, défini par
donnant la direction de propagation des rayons lumineux, défini par
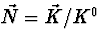 , il vient
, il vient
| 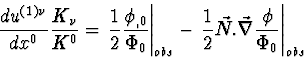 |
(82) |
où  désigne l'opérateur gradient.
désigne l'opérateur gradient.
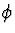 est une fonction d'une variable u (phase) que l'on peut écrire sous
la forme
est une fonction d'une variable u (phase) que l'on peut écrire sous
la forme
| 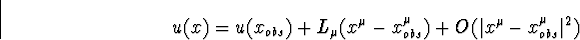 |
(83) |
avec
| 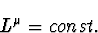 |
(84) |
Les relations (C.55) et (C.56) traduisent le fait que l'onde scalaire est
localement plane à l'observateur.
Les composantes spatiales Li indiquent la direction de propagation
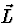 de l'onde scalaire à l'observateur. On a alors
de l'onde scalaire à l'observateur. On a alors
|  |
(85) |
avec 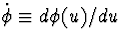 et
et 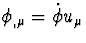 .
Soit
.
Soit 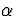 l'angle entre les directions
de propagation des rayons lumineux et de l'onde scalaire à l'observateur.
La relation (C.54) s'écrit en explicitant (C.57)
l'angle entre les directions
de propagation des rayons lumineux et de l'onde scalaire à l'observateur.
La relation (C.54) s'écrit en explicitant (C.57)
| 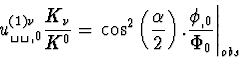 |
(86) |



Next: La scintillation.
Up: La scintillation.
Previous: Le terme spectral intégré.
11/13/1998
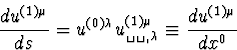
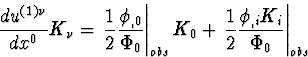
![]() donnant la direction de propagation des rayons lumineux, défini par
donnant la direction de propagation des rayons lumineux, défini par
![]() , il vient
, il vient