


Next: L'approximation des champs faibles.
Up: La scintillation.
Previous: Méthode de calcul.
Le potentiel vecteur complexe s'écrit
|  |
(37) |
où les réels 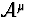 et S désignent respectivement
l'amplitude et la phase du rayonnement électromagnétique.
et S désignent respectivement
l'amplitude et la phase du rayonnement électromagnétique.
Les variations de l'amplitude sont lentes sur l'échelle de distance
considérée, contrairement aux variations de phase. Cette caractéristique
permet de développer 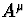 par rapport à un paramètre sans
dimension
par rapport à un paramètre sans
dimension 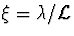 où
où 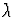 est la longueur d'onde
optique et
est la longueur d'onde
optique et 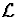 l'échelle typique sur laquelle l'amplitude varie de
manière appréciable (Misner et al. 1973).
Les solutions de (C.3) sont de la forme
l'échelle typique sur laquelle l'amplitude varie de
manière appréciable (Misner et al. 1973).
Les solutions de (C.3) sont de la forme
| ![\begin{displaymath}
A^{\mu} = [a^{\mu} + \xi b^{\mu} + \xi^2 c^{\mu} + ..] \exp
[\frac{i}{\xi} \hat{S}(x)]\end{displaymath}](img85.gif) |
(38) |
où 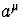 ,
, 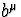 .. sont complexes et avec par définition
.. sont complexes et avec par définition
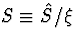 où
où 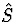 est indépendant de
est indépendant de 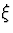 .
.
En reportant le développement (C.9) dans (C.3), il vient
| 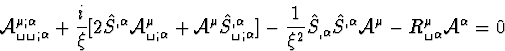 |
(39) |
On introduit le champ de vecteur
|  |
(40) |
pour lequel les rayons lumineux sont des courbes tangentes à 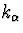 en
tout point. Le paramètre affine v le long d'un rayon lumineux
est tel que les composantes contravariantes
en
tout point. Le paramètre affine v le long d'un rayon lumineux
est tel que les composantes contravariantes 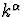 s'écrivent
s'écrivent
| 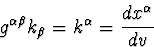 |
(41) |
L'approximation de l'optique géométrique consiste à faire tendre la
longueur d'onde optique 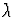 et ipso facto
et ipso facto 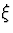 vers 0.
vers 0.
Les termes dominants de (C.10) sont les puissances négatives de
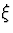 alors que l'amplitude
alors que l'amplitude 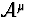 se réduit à son premier terme
se réduit à son premier terme
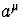 . (C.10) conduit en utilisant (C.11) et (C.12) aux équations
fondamentales suivantes de l'optique géométrique dans un espace-temps courbe
. (C.10) conduit en utilisant (C.11) et (C.12) aux équations
fondamentales suivantes de l'optique géométrique dans un espace-temps courbe
|  |
(42) |
| 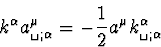 |
(43) |
La relation (C.13) traduit l'isotropie du vecteur d'onde:
les photons ont une masse nulle. Cette équation régit
l'évolution de la phase du rayonnement électromagnétique. En la
différentiant, et en remarquant que 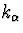 est le gradient d'une
fonction scalaire, il vient d'après (B.5)
est le gradient d'une
fonction scalaire, il vient d'après (B.5)
|  |
(44) |
qui est l'équation des géodésiques: les rayons
lumineux sont des géodésiques isotropes de l'espace-temps.
La relation (C.14) est l'équation d'évolution de l'amplitude du
potentiel vecteur. Soit l'amplitude scalaire
|  |
(45) |
le signe moins étant lié au caractère du genre espace de 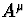 .
L'équation de propagation de a obtenue à partir de
(C.14) s'écrit
.
L'équation de propagation de a obtenue à partir de
(C.14) s'écrit
| 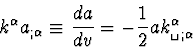 |
(46) |
où dv est l'élément différentiel le long
d'un rayon lumineux.
En faisant l'hypothèse que la perturbation n'atteint pas
la source lumineuse, dorénavant supposée à l'infini,
l'intégration de (C.17) le long d'un rayon lumineux donne
| 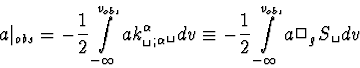 |
(47) |
où par définition, 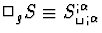 qui
s'identifie à
qui
s'identifie à 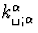 d'après (B.5) et (C.11).
L'indice g souligne qu'il du d'Alembertien sur l'espace courbe, qui
s'écrit, appliqué à une quantité scalaire F
d'après (B.5) et (C.11).
L'indice g souligne qu'il du d'Alembertien sur l'espace courbe, qui
s'écrit, appliqué à une quantité scalaire F
| 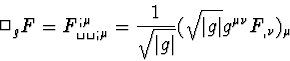 |
(48) |
où |g| est le déterminant de la métrique.
La relation (C.18) est exploitée au 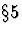 afin de discuter l'approche
classique de la scintillation par une perturbation matérielle.
afin de discuter l'approche
classique de la scintillation par une perturbation matérielle.
Une relation utile par la suite porte sur a2 dont l'équation
d'évolution est d'après (C.17)
| 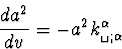 |
(49) |
À l'approximation de l'optique géométrique, la condition de jauge
(C.4) donne
| 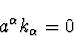 |
(50) |
Le tenseur (C.1) du champ électromagnétique se simplifie en
| ![\begin{displaymath}
F_{\mu \nu} = {\cal{R}}e(i[k_{\mu} a_{\nu} - k_{\nu} a_{\mu}]e^{iS}) \end{displaymath}](img108.gif) |
(51) |
ce qui amène à l'expression suivante du tenseur impulsion-énergie (C.5),
moyenné sur une période
| 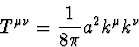 |
(52) |
Le flux d'énergie électromagnétique (C.7) sur le détecteur
s'écrit alors
| 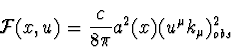 |
(53) |
L'énergie d'un photon mesurée par un observateur de quadrivitesse
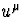 est
est 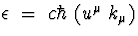 où
où 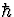 est la constante de Planck, d'où le flux de photons compté par
l'observateur de quadrivitesse
est la constante de Planck, d'où le flux de photons compté par
l'observateur de quadrivitesse 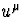
| 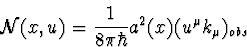 |
(54) |
qui s'exprime en fonction du décalage spectral z
(Ellis 1971) défini par
|  |
(55) |
soit
| 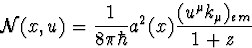 |
(56) |
Le second terme dans le membre de droite de (C.27) décrit des variations
spectrales dues aux changements de fréquence des photons à la
traversée de la perturbation gravitationnelle. Ces changements de
fréquence constituent une perturbation du décalage spectral cosmologique.
Les variations de a2 traduisent un effet
géométrique sur la section d'un faisceau lumineux, comme le montre la relation
suivante: soit 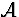 l'aire de la section d'un faisceau lumineux;
d'après Misner et al. (1973)
l'aire de la section d'un faisceau lumineux;
d'après Misner et al. (1973)
|  |
(57) |
Il est intéressant d'expliciter le terme géométrique en tant
qu'intégrale d'une certaine quantité le long de la ligne de visée.
Différentiant (C.20) par rapport à dv, il vient
| ![\begin{displaymath}
\frac{d^2 a^2(x,u)}{dv^2} = a^2(x,u) [(k^{\beta}_{\verb*+ +;\beta})^2 -
k^{\alpha} k^{\beta}_{\verb*+ +;\beta ;\alpha}] \end{displaymath}](img119.gif) |
(58) |
Le dernier terme s'écrit, en tenant compte de (B.6) et (C.15)
| 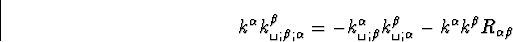 |
(59) |
En définissant 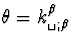 , et
, et
![$\vert\sigma\vert^2~=~[k^{\alpha}_{\verb*+ +;\beta}~k^{\beta}_
{\verb*+ +;\alpha}~+~\theta^2]$](img122.gif) , la relation (C.29) s'écrit
, la relation (C.29) s'écrit
| ![\begin{displaymath}
\frac{d^2 a^2}{dv^2} = a^2
[\vert\sigma\vert^2 + k^{\alpha} k^{\beta} R_{\alpha \beta}]\end{displaymath}](img123.gif) |
(60) |
Cette équation est généralement présentée sous la forme d'une
équation portant sur la longueur 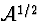 . L'équation de
propagation de
. L'équation de
propagation de 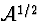 est obtenue à partir de (C.28) et (C.17).
Elle s'écrit
est obtenue à partir de (C.28) et (C.17).
Elle s'écrit
| 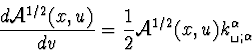 |
(61) |
Un calcul analogue à celui mené pour obtenir (C.31) conduit à
| ![\begin{displaymath}
\frac{d^2 {\cal{A}}^{1/2} }{dv^2} = - {\cal{A}}^{1/2}
[\ver...
...gma'\vert^2 + \frac{1}{2}k^{\alpha} k^{\beta} R_{\alpha \beta}]\end{displaymath}](img126.gif) |
(62) |
avec
![$\vert\sigma'\vert^2~=~[\frac{1}{2}k^{\alpha}_{;\beta}~k^{\beta}_{;\alpha}~-~\frac{1}{4}
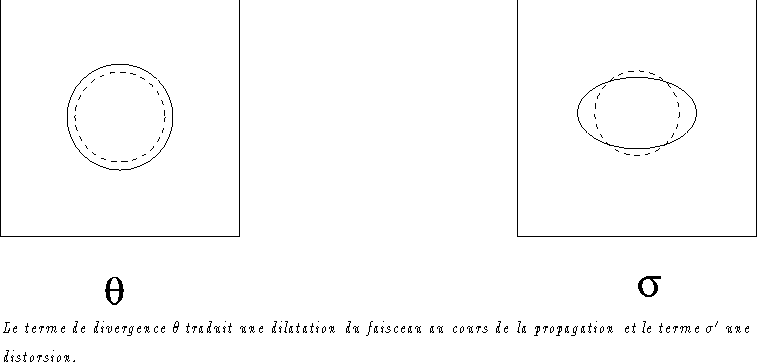
\theta^2]$](img127.gif) . C'est l'équation fondamentale décrivant l'effet d'une
perturbation gravitationnelle
sur la géométrie d'un faisceau lumineux (Sachs 1961, Misner et al.
1973), cf. Fig.C.2.
. C'est l'équation fondamentale décrivant l'effet d'une
perturbation gravitationnelle
sur la géométrie d'un faisceau lumineux (Sachs 1961, Misner et al.
1973), cf. Fig.C.2.
Le tenseur de Ricci, lié au contenu énergétique de
l'espace-temps par les équations d'Einstein (B.8), traduit une propriété
focalisante de la matière.
Figure:
Plan de coupe d'un faisceau de rayons lumineux.
 |



Next: L'approximation des champs faibles.
Up: La scintillation.
Previous: Méthode de calcul.
11/13/1998
![]() par rapport à un paramètre sans
dimension
par rapport à un paramètre sans
dimension ![]() où
où ![]() est la longueur d'onde
optique et
est la longueur d'onde
optique et ![]() l'échelle typique sur laquelle l'amplitude varie de
manière appréciable (Misner et al. 1973).
Les solutions de (C.3) sont de la forme
l'échelle typique sur laquelle l'amplitude varie de
manière appréciable (Misner et al. 1973).
Les solutions de (C.3) sont de la forme
![\begin{displaymath}
A^{\mu} = [a^{\mu} + \xi b^{\mu} + \xi^2 c^{\mu} + ..] \exp
[\frac{i}{\xi} \hat{S}(x)]\end{displaymath}](img85.gif)
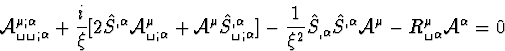
![]() et ipso facto
et ipso facto ![]() vers 0.
vers 0.
![]() alors que l'amplitude
alors que l'amplitude ![]() se réduit à son premier terme
se réduit à son premier terme
![]() . (C.10) conduit en utilisant (C.11) et (C.12) aux équations
fondamentales suivantes de l'optique géométrique dans un espace-temps courbe
. (C.10) conduit en utilisant (C.11) et (C.12) aux équations
fondamentales suivantes de l'optique géométrique dans un espace-temps courbe
![]() est le gradient d'une
fonction scalaire, il vient d'après (B.5)
est le gradient d'une
fonction scalaire, il vient d'après (B.5)
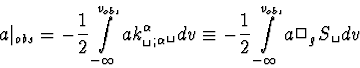
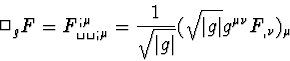
![]() afin de discuter l'approche
classique de la scintillation par une perturbation matérielle.
afin de discuter l'approche
classique de la scintillation par une perturbation matérielle.
![]() est
est ![]() où
où ![]() est la constante de Planck, d'où le flux de photons compté par
l'observateur de quadrivitesse
est la constante de Planck, d'où le flux de photons compté par
l'observateur de quadrivitesse ![]()

![]() l'aire de la section d'un faisceau lumineux;
d'après Misner et al. (1973)
l'aire de la section d'un faisceau lumineux;
d'après Misner et al. (1973)
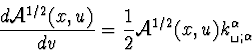
![\begin{displaymath}
\frac{d^2 {\cal{A}}^{1/2} }{dv^2} = - {\cal{A}}^{1/2}
[\ver...
...gma'\vert^2 + \frac{1}{2}k^{\alpha} k^{\beta} R_{\alpha \beta}]\end{displaymath}](img126.gif)