[ Présentation d'Aurélie |
Guide Pratique |
Page d'accueil OHP ]
AURELIE : the high resolution spectrometer of the Haute-Provence
Observatory
AURELIE : the high resolution spectrometer
of the Haute-Provence Observatory
D. Gillet, R. Burnage, D. Kohler, D. Lacroix, G. Adrianzyk,
J.C. Baietto, J.P. Berger, M. Goillandeau, C. Guillaume, C. Joly, J.P.
Meunier, G. Rimbaud, and A. Vin.
Astronomy & Astrophysics Supplements (1994) vol.108, p.181
Abstract. A powerful and simple high resolution spectrometer
has been developed and installed in 1989 at the Haute-Provence Observatory
on the 1.52 m
telescope. It was designed primarily for high resolution (50 000 <
R
< 110 000) spectroscopy of point-like sources but medium resolutions
down to
5 000 are also available. The use of a Thomson TH 7832, a linear array
CCD-like
detector, provides the benefit of a very clean detector (no interference
fringes or persistence effects). Due to the average seeing at OHP, a
modified Bowen-Walraven image-slicer was used. The stability of the
spectrometer is discussed together with its astrophysical performances.
Keywords : Instrumentation : spectrographs - Instrumentation :
detectors - Line : profiles - Stars :
general
Introduction
The largest telescopes being mainly devoted to extragalactic objects,
a vast majority of stellar studies of individual stars are done with
2m-class telescopes. This is true particularly for spectroscopic researches.
Scientifically speaking this is not fully justified and it is a pity
that allocating time committees sometimes think more in magnitude than
in erg s-1 Å-1 px-1.
Nevertheless, the physical phenomena occurring in stellar atmospheres
often require a lot of observing time because of their long or very
long characteristic time scale. Studies of such variable phenomena can
therefore only be carried out with relatively small telescopes. This
means that small telescopes still have an important role to play for
the foreseeable future.
For decades, all spectroscopic observations have been realized with
photographic plates. Since the relatively recent appearance of modern
detectors like CCDs, the efficiency of spectrographs has been mutiplied
by 10 or more. This is also the consequence of numerous progresses in
optics during the last 20 years. In addition the photometric quality
of the spectra obtained with modern detectors has allowed to study line
profiles as never before.
For all these reasons, many astronomical spectrographs have been designed
especially for high resolution spectroscopy. In 1986, it became urgent
to develop a high-performance high-resolution spectrometer at the Haute-Provence
Observatory (OHP). At that time, OHP-telescopes were fitted with two
large spectrographs: the so-called REOSC at the 1.93 m telescope and
the ECHELEC at the 1.52 m telescope. The first used the photographic
plate as detector as the second used the Lallemand electronic camera
(Baranne & Duchesne 1976). Recently the 1.93 m telescope was equiped
with a new low resolution spectrometer (CARELEC, Lemaitre et al. 1990)
with a CCD detector. Thus the construction of a high resolution spectrometer
at the 1.52 m telescope became a priority. The aim of this paper is
to present this new spectrograph.
In Section 2
we give design considerations and a description of the optical layout.
Section 3
is devoted to the detector while
Section 4
analyses the performances of the whole instrument including the detector.
Finally, we give some concluding remarks in the last section.
Optics
The optical concept
The optical concept of AURELIE results from a compromise to best satisfy
the four following conditions:
- both medium and high spectral resolution configurations must
be easily and
rapidly operational over the whole spectral domain of sensitivity of
the detector (3900 to 10 000 Å). Of course the precise repositioning
of the mechanical and optical elements of the spectrograph must reach
an accuracy high enough to allow a reproducibility consistent with the
desired mechanical and optical stability.
- preserving for each configuration the largest possible spectral
domain to
determine the best stellar continuum.
- obtaining the largest optical efficiency and a very small amount
of scattered light. At OHP this necessarily implies the use of an entrance
aperture about 3 arcsec wide given the average seeing conditions. During
the detailed engineering phase we have always tried to minimize the
number of optical elements and to use the best surface treatments available.
- designing an instrument of modest dimensions to reduce aberrations
especially the spherical one, and to save money.
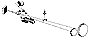 Fig.1a
The use of a modified Bowen-Walraven image-slicer (Walraven and Walraven
1972, Lund and Ferlet 1984), together with a long focal length (1 m)
camera and a detector having a large number (2048) of small size (13
µm) pixels, was found to be a good solution. Indeed, to obtain
the same resolving power with an entrance aperture of 3 arcsec and without
image-slicer, an unreasonable pupil diameter of 500 mm and an aperture
of camera of f/2 would be required. The general principle of the instrument
is classical (see Fig.1a, Fig.1b).
Fig.1a
The use of a modified Bowen-Walraven image-slicer (Walraven and Walraven
1972, Lund and Ferlet 1984), together with a long focal length (1 m)
camera and a detector having a large number (2048) of small size (13
µm) pixels, was found to be a good solution. Indeed, to obtain
the same resolving power with an entrance aperture of 3 arcsec and without
image-slicer, an unreasonable pupil diameter of 500 mm and an aperture
of camera of f/2 would be required. The general principle of the instrument
is classical (see Fig.1a, Fig.1b).
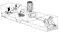 Fig.1b
The collimator and the camera are two spherical mirrors and the grating
is located at their common curvature center. The aperture of the collimator
and the camera are f/10 for a pupil diameter of 100 mm. 100% of the
residual spherical aberration produced by the whole optical system before
the cylindrical lens is in a circle of 19 µm in diameter.
Fig.1b
The collimator and the camera are two spherical mirrors and the grating
is located at their common curvature center. The aperture of the collimator
and the camera are f/10 for a pupil diameter of 100 mm. 100% of the
residual spherical aberration produced by the whole optical system before
the cylindrical lens is in a circle of 19 µm in diameter.
 Fig.2
After the cylindrical lens, the spot-diagrams (Fig.2) show that it is
not beneficial to correct the field curvature because it is not the
same for different points of the entrance slit. The optical transmission
Ts of the spectrometer, ignoring the grating and the filter
isolating the order to be observed, is 0.41 ± 0.04 at 4000 Å,
and 0.52 ± 0.04 at 5500 Å. If we take them into account then
it varies between 0.06 and 0.40 depending on the AURELIE configuration.
Fig.2
After the cylindrical lens, the spot-diagrams (Fig.2) show that it is
not beneficial to correct the field curvature because it is not the
same for different points of the entrance slit. The optical transmission
Ts of the spectrometer, ignoring the grating and the filter
isolating the order to be observed, is 0.41 ± 0.04 at 4000 Å,
and 0.52 ± 0.04 at 5500 Å. If we take them into account then
it varies between 0.06 and 0.40 depending on the AURELIE configuration.
Field acquisition and automatic guiding on the entrance hole are effected
thanks to a tilted (7.5°) and centre-holed (600 µm) mirror.
This optical system is equipped with a CCD camera which requires the
use of a neutral density wheel. Several calibration lamps are available.
For wavelength calibrations, Th-Ne, Th-Ar or Fe-Ne hollow cathode lamps
can be used while the photometric correction (flat field) is provided
by a W-lamp. An optional exposure meter is also available. A chopper
(5 Hz), located in front of the image-slicer, takes about 5% of the
stellar flux.
The image-slicer
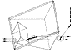 Fig.3
AURELIE is dedicated to the 1.52 m Coudé telescope which has
a focal ratio of f/27.6. The entrance is a hole of 600 µm i.e.,
3 arcsec on the sky. To reach a high resolving power without loosing
too much light, we have used a modified Bowen-Walraven image-slicer.
Fig.3 shows its schematic diagram ; its optical description is
given by Walraven and Walraven (1972) and by Lund and Ferlet (1984).
Note that a circular entrance has been used instead a square-shaped
one as required by this type of image-slicer. Although this choice must
produce a small loss of the starlight, it was only motivated by a practical
point of view : the drilling of the centre-holed mirror. The circular
starlight image is cut into 5 slices of 0.6 arcsec on the sky. The optical
transmission of the image-slicer with a single-layer reflectance coating
is 0.90 ± 0.02. It has been necessary to enlarge 3.62 times the
input star image to allow an easy building. This enlargement also implies
that the image-slicer works with an entrance focal ratio of f/100. Although
this last value is not presently justified by a complete optical calculation
which is outside of our actual capabilities, it reduces the difference
in focus of the successive slices to quite an acceptable value. The
pupil is imaged out at infinity before the entrance of the image-slicer
and is reconstructed at its exit. Nevertheless it is affected by diffraction
due to the small width of the "equivalent" slit (0.6 arcsec). Otherwise
it is possible to estimate that the error in wavelength induced by
a bad centering of the star on the 3 arcsec entrance hole, is of the
same order of magnitude than if a slit of 0.6 arcsec was actually used.
This last point is important in the measurement of radial velocities.
Fig.3
AURELIE is dedicated to the 1.52 m Coudé telescope which has
a focal ratio of f/27.6. The entrance is a hole of 600 µm i.e.,
3 arcsec on the sky. To reach a high resolving power without loosing
too much light, we have used a modified Bowen-Walraven image-slicer.
Fig.3 shows its schematic diagram ; its optical description is
given by Walraven and Walraven (1972) and by Lund and Ferlet (1984).
Note that a circular entrance has been used instead a square-shaped
one as required by this type of image-slicer. Although this choice must
produce a small loss of the starlight, it was only motivated by a practical
point of view : the drilling of the centre-holed mirror. The circular
starlight image is cut into 5 slices of 0.6 arcsec on the sky. The optical
transmission of the image-slicer with a single-layer reflectance coating
is 0.90 ± 0.02. It has been necessary to enlarge 3.62 times the
input star image to allow an easy building. This enlargement also implies
that the image-slicer works with an entrance focal ratio of f/100. Although
this last value is not presently justified by a complete optical calculation
which is outside of our actual capabilities, it reduces the difference
in focus of the successive slices to quite an acceptable value. The
pupil is imaged out at infinity before the entrance of the image-slicer
and is reconstructed at its exit. Nevertheless it is affected by diffraction
due to the small width of the "equivalent" slit (0.6 arcsec). Otherwise
it is possible to estimate that the error in wavelength induced by
a bad centering of the star on the 3 arcsec entrance hole, is of the
same order of magnitude than if a slit of 0.6 arcsec was actually used.
This last point is important in the measurement of radial velocities.
The cylindrical lens in front of the detector
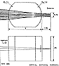 Fig.4
The monochromatic geometrical image at the camera focus largely overflows
the detector height (1.07 mm for 0.75mm). Consequently a silica cylindrical
lens made of a small bar 5 mm in diameter (Fig.4) and located very close
to the detector, forms along the detector length the dispersed image
of the slit and, perpendicularly, the pupil of the instrument. First
this lens allows to adjust the spectrum height to that of the detector.
It keeps also a constant illumination over the pixel height when the
star is decentered or when the seeing changes. Finally the last advantage,
the setting of the grating angle in the direction perpendicular to the
dispersion, for instance after a grating change, is much less critical.
The use of this cylindrical lens does not appreciably impair the resolution
of the instrument if, during its mounting in the CCD cryostat, the parallelism
between the axis of the cylindrical lens and the detector is good enough
(tolerance ± 30'). Indeed, the overall width of the spot-diagrams
remains between 19 µm and 27 µm in the field. To get an accurate
estimate of the resulting resolution, it should be necessary to add
the spot-diagrams coming from all points of the slit and to do a vertical
integration. A rigorous computation should take into account diffraction
effects which must be significant at the image extremities where the
beam aperture tends to zero. We have observed a widening of the extremities
of the images in laboratory but a quantitative analysis was not possible
at that time. A motorized mechanical device also gives the possibility
to shift and rotate the cryostat around its axis to get a good coincidence
between the detector and the spectrum. This mechanism is locked during
the observations.
Fig.4
The monochromatic geometrical image at the camera focus largely overflows
the detector height (1.07 mm for 0.75mm). Consequently a silica cylindrical
lens made of a small bar 5 mm in diameter (Fig.4) and located very close
to the detector, forms along the detector length the dispersed image
of the slit and, perpendicularly, the pupil of the instrument. First
this lens allows to adjust the spectrum height to that of the detector.
It keeps also a constant illumination over the pixel height when the
star is decentered or when the seeing changes. Finally the last advantage,
the setting of the grating angle in the direction perpendicular to the
dispersion, for instance after a grating change, is much less critical.
The use of this cylindrical lens does not appreciably impair the resolution
of the instrument if, during its mounting in the CCD cryostat, the parallelism
between the axis of the cylindrical lens and the detector is good enough
(tolerance ± 30'). Indeed, the overall width of the spot-diagrams
remains between 19 µm and 27 µm in the field. To get an accurate
estimate of the resulting resolution, it should be necessary to add
the spot-diagrams coming from all points of the slit and to do a vertical
integration. A rigorous computation should take into account diffraction
effects which must be significant at the image extremities where the
beam aperture tends to zero. We have observed a widening of the extremities
of the images in laboratory but a quantitative analysis was not possible
at that time. A motorized mechanical device also gives the possibility
to shift and rotate the cryostat around its axis to get a good coincidence
between the detector and the spectrum. This mechanism is locked during
the observations.
Gratings
 Fig.5a
Seven gratings are available giving a wide range of resolving powers.
Fig.5a gives the characteristics of the eight possible configurations.
Each grating is mounted on a pre-setting support to warrant that the
position of the spectrum varies very little when the central wavelength
or the grating is changed.
Fig.5a
Seven gratings are available giving a wide range of resolving powers.
Fig.5a gives the characteristics of the eight possible configurations.
Each grating is mounted on a pre-setting support to warrant that the
position of the spectrum varies very little when the central wavelength
or the grating is changed.
 Fig.5b
The gratings are manually interchangeable; they are set on a goniometric
turn-table by a dynanometric spanner. The goniometric unit ensures an
angular positional accuracy of 1/1000 of a degree. Thus the final uncertainty
on the required central wavelength does not exceed ± 10 pixels
corresponding to 0.5% of the available wavelength range. The spectra
are perfectly rectilinear and the spectral lines given with the image-slicer
are perpendicular to the dispersion.
Fig.5b
The gratings are manually interchangeable; they are set on a goniometric
turn-table by a dynanometric spanner. The goniometric unit ensures an
angular positional accuracy of 1/1000 of a degree. Thus the final uncertainty
on the required central wavelength does not exceed ± 10 pixels
corresponding to 0.5% of the available wavelength range. The spectra
are perfectly rectilinear and the spectral lines given with the image-slicer
are perpendicular to the dispersion.
 Fig.6
shows the absolute efficiency of the AURELIE gratings versus wavelength.
The different symbols represent the measurements made in laboratory
from which we have determined the best working zones (thick lines in
Fig.5b).
Fig.6
shows the absolute efficiency of the AURELIE gratings versus wavelength.
The different symbols represent the measurements made in laboratory
from which we have determined the best working zones (thick lines in
Fig.5b).
Inside them, the efficiency is larger or equal to 2/3 of the maximum
grating efficiency except for the Echelle grating. For the latter, the
absolute
efficiency is between 40 and 65% depending of the departure from the
blaze angle. It is used between orders 25 and 60.
The detector
The double linear array TH 7832, first presented by Coutures and Boucharlat
(1988a and 1988b), is made of two identical independant arrays. Only
one is used for the AURELIE spectrometer. In the following, when using
the term "array", we shall refer to the one array used in the spectrometer.
The array is made of 2048 photodiodes of which 2036 are usable. The
pixels of odd order are coupled to a CCD register referred to as channel
1, those of even order are coupled to another CCD register referred
to as channel 2. At reading time, the charges are transferred from the
photodiodes to the CCD registers and are read serially through two identical
but physically different electronic systems output1 and output2. Though
they have been adjusted to give similar results, the amplifications
of both outputs are not identical. This is well corrected by flatfielding,
the linearity of both systems being quite good from
0 ADU above offset (ADU = Analogue-to-Digital Unit) up to saturation
(28 000 ADU).
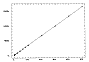 Fig.7a
Figures 7a and 7b show the linearity of channel 1 between 0 and 16 000
ADU but
it is still acceptable up to 28 000 ADU. Fig.7a displays the linear
regression linking integration-time and signal for frames taken with
the same illumination and different integration-times.
Fig.7a
Figures 7a and 7b show the linearity of channel 1 between 0 and 16 000
ADU but
it is still acceptable up to 28 000 ADU. Fig.7a displays the linear
regression linking integration-time and signal for frames taken with
the same illumination and different integration-times.
 Fig.7b
The residuals (multiplied by 1000) versus the observed signal are presented
in Fig.7b.
The deviation from linearity are smaller than 1% above a signal of
1000 ADU; observers generally work above 1000 ADU
(S/N
Fig.7b
The residuals (multiplied by 1000) versus the observed signal are presented
in Fig.7b.
The deviation from linearity are smaller than 1% above a signal of
1000 ADU; observers generally work above 1000 ADU
(S/N  80).
80).
The gain of each channel has been adjusted as to be very much the same.
It is
presently 39.5 e- /ADU.
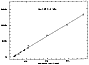 Fig.8
shows the relation between the variance measured on the difference
of pairs of identical flatfields and the average signal for channel
1.
Fig.8
shows the relation between the variance measured on the difference
of pairs of identical flatfields and the average signal for channel
1.
Both channels do not have the same read-out-noise : 343 e-
for channel 1 and 264 e- for channel 2. Contrary to ordinary
CCDs, the noise induced by the pixel capacity (which depends on its
area), is the dominant noise source for the TH 7832. The high value
of the measured read-out-noise is due to the large pixel
size
(13x750 µm2).
The offset value varies with time after pumping the dewar in which
it is located. The typical value just after pumping is 200 ADU and may
reach some 250 ADU after one month. During the night it may change by
a few ADU in an unpredictable way. Small deformations of the offset
pattern also occur but it remains quite constant overnight. These unstabilities
are possibly due to an extreme sensitivity of the chip to temperature,
the degradation of the vacuum in the dewar modifying the thermal equilibrium
of the detector. It is therefore wise to take series of offset from
time to time during the night, the whole process only takes a few minutes.
The dark current varies in the opposite way, from 20 ADU/h after pumping,
decreasing to 0 ADU/h after 12 days.
The array presently used has a big flaw between pixels 1500 and 1800.
This is
well corrected by flatfielding; however we observe some residual modulations
with a 1% amplitude around the resulting signal.
 Fig.9
The quantum efficiency is given in Fig.9. It was calculated from measurements
of spectral response realized by Coutures and Boucharlat (1987) on several
TH 7832 arrays. The continuous line represents the average typical quantum
efficiency while the dashed line shows an actual exemple. A strong wavelength
modulation is visible. It is mainly due to multiple reflections occurring
within the SiO2 layer of 1.5 µm ± 0.1 thickness
located above the photodiodes.
Fig.9
The quantum efficiency is given in Fig.9. It was calculated from measurements
of spectral response realized by Coutures and Boucharlat (1987) on several
TH 7832 arrays. The continuous line represents the average typical quantum
efficiency while the dashed line shows an actual exemple. A strong wavelength
modulation is visible. It is mainly due to multiple reflections occurring
within the SiO2 layer of 1.5 µm ± 0.1 thickness
located above the photodiodes.
During the development and testing of the detector and then during
its astronomical use, no persistence effect induced by a prior and strong
illumination has been noted. Moreover no interference pattern (which
is most severe in the red/IR region of most CCDs) is observed on the
TH 7832. This last point, as shown in
Section 4,
5,
constitutes an appreciable benefit to detect very weak absorption lines.
Performances
Instrumental stability
It is most interesting to evaluate the order of magnitude of the smallest
line shifts that the spectrometer can detect. From the analysis of the
fluctuations observed in a series of measurements of the distance between
two Th-lines, it was possible to estimate the measurement accuracy :
± 0.02 pixel, corresponding to ± 0.26 µm on the detector
and to ± 0.03 arcsec of the grating rotation!
During the conception and the construction of AURELIE a lot of precautions
have been taken to limit all possible instrumental instabilities. For
instance thermal exchanges between the calibration lamps and the spectrometer
or those induced by the cryostat were suppressed or reduced to an acceptable
level. Although the Coudé room is air-conditioned, thermal phenomena
are expected to represent the main source of instrumental instabilities.
If we neglect the hygrometry effect, the shift

 caused by variations of the air index n and dilatation of the
grating blank is
given by
caused by variations of the air index n and dilatation of the
grating blank is
given by
{equation 1}



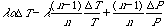 ,
,
where T is the temperature, P the atmospheric
pressure
and  the dilatation coefficient of the grating (4.5 · 10-6
for ZKN7 blank
and 8 · 10-6 for BSC2 blank).
Assuming the air index at 20°C and 710 mmHg to be equal to
the dilatation coefficient of the grating (4.5 · 10-6
for ZKN7 blank
and 8 · 10-6 for BSC2 blank).
Assuming the air index at 20°C and 710 mmHg to be equal to
{equation 2}
(n -1)
 0.255 · 10-3,
0.255 · 10-3,
we finally obtain
{equation 3}



 [(
[( - 0.87 · 10-6)
- 0.87 · 10-6)
 T + 0.36 · 10-6
T + 0.36 · 10-6
 P ],
P ],
with P in mmHg. The atmospheric pressure variations are
seldom larger
than 0.5 mmHg/h. Consequently, from Eq. (3), it appears that the main
source of instability is due to temperature variations. This is due
to the fact that the thermal regulation of AURELIE is not extremely
sophisticated and we do not use a grating blank having a zero dilatation
coefficient. With
 P = 0 and T
= 20° C,
Eq. (3) reduces to
P = 0 and T
= 20° C,
Eq. (3) reduces to
{equation 4}

 px/°C
px/°C 
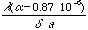 ,
,
where the shift

 is expressed in pixel /°C.
is expressed in pixel /°C.  is in Å, the reciprocal linear dispersion
is in Å, the reciprocal linear dispersion
 in Å/mm and the pixel width a in mm.
in Å/mm and the pixel width a in mm.
 Fig.10
If we apply this last expression to the most commonly used AURELIE gratings
(Fig.10),
it appears that the dilatation coefficient of the grating blank is of
utmost importance.
Fig.10
If we apply this last expression to the most commonly used AURELIE gratings
(Fig.10),
it appears that the dilatation coefficient of the grating blank is of
utmost importance.
A systematic study of the stability of the position of Th-lines show
that, in
general, variations smaller or equal to 0.1 px/hr are present. Of course
this
measurement includes all possible effects. Thus, since the Coudé
room
temperature does not change by more than 0.2 °C/hr, it appears
that the
above theoretical discussion is consistent with our experimental result.
This
also means that the main source of the instrumental instability is due
to the
sensitivity to global temperature changes. A more quantitative modelisation
of
the wavelength stability depends on the actual temperature profile to
which the
instrument is subjected via the Coudé room temperature variations.
This
needs to know the response of the instrument to mechanical deformations
due to
temperature gradients. This study is outside the scope of this paper.
Resolution
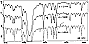 Fig.11
AURELIE can be used in 8 different resolving configurations
(see Fig.3) from
R = 4 000 (
Fig.11
AURELIE can be used in 8 different resolving configurations
(see Fig.3) from
R = 4 000 (

 60 km/s)
to R =110 000 000 (
60 km/s)
to R =110 000 000 (

 3 km/s).
Figure 11 shows the spectrum around
H
3 km/s).
Figure 11 shows the spectrum around
H of the star
HR 3459 (V = 4.63, G2 Ib,
T
of the star
HR 3459 (V = 4.63, G2 Ib,
T
 5400 K,
5400 K,
 sin i = 8 km/s)
observed with the classical gratings number 2 (1200 l/mm, 7.8 Å/mm)
and number 5 in the second order (1200 l/mm, 2.7 Å/mm), and the
Echelle grating number 6 (79 l/mm, 1.9 Å/mm). The resolving powers
R measured by the FWHM of unblended and unsaturated thorium lines are
respectively 21 000, 70 000 and 110 000 which
correspond to 2.94, 2.60 and 2.40 pixels.
sin i = 8 km/s)
observed with the classical gratings number 2 (1200 l/mm, 7.8 Å/mm)
and number 5 in the second order (1200 l/mm, 2.7 Å/mm), and the
Echelle grating number 6 (79 l/mm, 1.9 Å/mm). The resolving powers
R measured by the FWHM of unblended and unsaturated thorium lines are
respectively 21 000, 70 000 and 110 000 which
correspond to 2.94, 2.60 and 2.40 pixels.
Signal-to-noise ratio and limiting magnitude
The entrance aperture on the sky is circular and has a diameter of 3
arcsec.
With such a large aperture and taking into account the average seeing
conditions at OHP, it is usual to collect 80% of the light. Of course
the instrumental efficiency is strongly dependent on the variation of
the seeing conditions during the integration time. Thus any estimate
of the signal-to-noise ratio must be used with caution. Hereafter we
have assumed that all the stellar flux is captured by the aperture ;
this means that our estimate corresponds to an upper limit of the AURELIE
efficiency.
The signal S in e- s-1 px-1
is given by
{equation 5}
S = F Tat St Tt Ts Tc
Tat St Tt Ts Tc

 ,
,
where
Note that because the stars considered are usually brigther than magnitude
10,
the sky background contribution can be neglected. The noise N
in e- px-1 is given by
{equation 6}
N = (ST + pR2 + DT )
1/2 ,
where the first term is the photon noise (T is the integration
time in s), the second term is the effective read-out-noise (ERON) and
D the dark current which is negligible here
(see Section 3).
Finally the signal-to-noise ratio is expressed by
{equation 7}
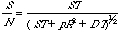 ,
,
where R  300 e-
and
p is a factor which depends on the number of flat fields
(FF) and fix pattern signals (FP) taken in sets and averaged to produce
a reduced-noise composite. With single FF and FP exposures, then the
ERON is
2R (p = 4)
while if we use, as usually, n FF and n FP,
the ERON becomes
300 e-
and
p is a factor which depends on the number of flat fields
(FF) and fix pattern signals (FP) taken in sets and averaged to produce
a reduced-noise composite. With single FF and FP exposures, then the
ERON is
2R (p = 4)
while if we use, as usually, n FF and n FP,
the ERON becomes
 p R
where p = (3+n ) / n
if the stellar signal and the FF one have about the same level. In any
case,
1
p R
where p = (3+n ) / n
if the stellar signal and the FF one have about the same level. In any
case,
1  p
p  4.
4.
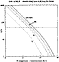 Fig.12
gives the S/N curve for grating number 5 in the second
order at 6 000 Å. The S/N ratio is largely detector
noise limited for
S/N < 70 while the photon noise dominates above S/N
>
400. When a S/N > 50 is required, the operational limiting
V-magnitude is between 6.4 and 9.9 for integration times between 5 and
120 min respectively. Table 1 gives the limiting V-magnitudes for all
other AURELIE configurations. Remember again that, because we have assumed
that the air mass is unity and all the starlight is collected by the
entrance hole, these limiting magnitudes constitute an upper limit.
An average atmospheric absorption coefficient was taken. It is also
clear that this estimate refers to a S/N calculated at
the stellar continuum. Thus the limiting magnitude can be appreciably
greater for the study of emission line objects such as planetary nebulae
or some variable stars.
Fig.12
gives the S/N curve for grating number 5 in the second
order at 6 000 Å. The S/N ratio is largely detector
noise limited for
S/N < 70 while the photon noise dominates above S/N
>
400. When a S/N > 50 is required, the operational limiting
V-magnitude is between 6.4 and 9.9 for integration times between 5 and
120 min respectively. Table 1 gives the limiting V-magnitudes for all
other AURELIE configurations. Remember again that, because we have assumed
that the air mass is unity and all the starlight is collected by the
entrance hole, these limiting magnitudes constitute an upper limit.
An average atmospheric absorption coefficient was taken. It is also
clear that this estimate refers to a S/N calculated at
the stellar continuum. Thus the limiting magnitude can be appreciably
greater for the study of emission line objects such as planetary nebulae
or some variable stars.
Table 1. Maximum expected limiting V-magnitude reached with
the various
AURELIE gratings for a signal-to-noise ratio S/N = 50 and
integration times of 5, 30, 60 and 120 min for an A0 V star.
| Grating |
 (Å) (Å)
|
integration time (min) |
| 5 |
30 |
60 |
120 |
| N°4 |
300 l/mm order I |
4500
6000 |
9.2
9.7 |
11.1
11.6 |
11.8
12.4 |
12.6
13.1 |
| N°3 |
600 l/mm order I |
4000
6000 |
8.9
8.7 |
10.9
10.7 |
11.6
11.4 |
12.4
12.2 |
| N°2 |
1200 l/mm order I |
4000
6000 |
8.0
7.9 |
9.9
9.8 |
10.7
10.6 |
11.4
11.3 |
| N°5 |
1200 l/mm order I |
6300
8000 |
7.6
7.3 |
9.6
9.3 |
10.3
9.9 |
11.1
10.8 |
| N°7 |
1800 l/mm order I |
4000
6000 |
7.6
7.0 |
9.6
8.9 |
10.3
9.7 |
11.1
10.4 |
| N°5 |
1200 l/mm order II |
4500
6000 |
6.8
6.4 |
8.7
8.4 |
9.4
9.1 |
10.2
9.9 |
| N°1 |
3000 l/mm order I |
4000
5500 |
6.3
5.8 |
8.2
7.8 |
8.9
8.4 |
9.7
9.3 |
| N°6 |
79 l/mm Echelle |
4000
6000
8000 |
4.5
5.9
5.7 |
6.4
7.9
7.7 |
7.2
8.6
8.4 |
7.9
9.4
9.2 |
Comparison with the ESO-CES
From the point of view of the signal-to-noise ratio, the most performant
configuration of the Coudé Echelle Spectrometer (CES) linked
to the 1.4 m Coudé Auxiliary Telescope (CAT) at the European
Southern Observatory (ESO, Chile ; Enard 1982) is the "short camera"
equiped with a RCA-CCD of 15 µm of pixel width.
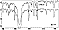 Fig.13
shows the same star HR 3459 as in
Fig.11 but observed both with AURELIE and CES.
The measured resolving power is practically the same
(R = 70 000 ± 500)
on the two spectra. Except for the position and intensity of the telluric
lines (mainly H2O), the spectra are very similar. If we take
into account the different diameters of the telescopes (1.40 and 1.52
m), the respective average atmospheric absorptions (0.05 and 0.10),
the integration times and the air masses during each observation, the
measured signal-to-noise ratios (230 and 300) show that both spectrometers
have similar efficiencies. In both cases, the photon noise regime was
dominant. Due to the AURELIE larger read-out-noise
(~ 300 e-) instead of (80 e-), we should expect
a better limiting magnitude with the CES.
Fig.13
shows the same star HR 3459 as in
Fig.11 but observed both with AURELIE and CES.
The measured resolving power is practically the same
(R = 70 000 ± 500)
on the two spectra. Except for the position and intensity of the telluric
lines (mainly H2O), the spectra are very similar. If we take
into account the different diameters of the telescopes (1.40 and 1.52
m), the respective average atmospheric absorptions (0.05 and 0.10),
the integration times and the air masses during each observation, the
measured signal-to-noise ratios (230 and 300) show that both spectrometers
have similar efficiencies. In both cases, the photon noise regime was
dominant. Due to the AURELIE larger read-out-noise
(~ 300 e-) instead of (80 e-), we should expect
a better limiting magnitude with the CES.
Three illustrative observations
 Fig.14
The star
Fig.14
The star  Peg (V = 4.79, A1 IV,
Peg (V = 4.79, A1 IV,
 sin i = 15 km/s)
was observed by T. Lanz (Geneva Observatory) around 6150 Å, on
December 1, 1989 (integration time of 30 min). The grating N° 5
in its second order provided the spectrum at a reciprocal linear dispersion
of 2.6 Å/mm giving a resolving power near 70 000. The signal-to-noise
ratio was estimated around 400. At this S/N level and
thanks to the absence of interference fringes, the detection of very
weak lines is possible. For instance, the Cr II
sin i = 15 km/s)
was observed by T. Lanz (Geneva Observatory) around 6150 Å, on
December 1, 1989 (integration time of 30 min). The grating N° 5
in its second order provided the spectrum at a reciprocal linear dispersion
of 2.6 Å/mm giving a resolving power near 70 000. The signal-to-noise
ratio was estimated around 400. At this S/N level and
thanks to the absence of interference fringes, the detection of very
weak lines is possible. For instance, the Cr II

 6147.15
absorption line which has an equivalent width
W
6147.15
absorption line which has an equivalent width
W  of 1.4 mÅ,
is well observed (Fig.14).
The probable internal error on W
of 1.4 mÅ,
is well observed (Fig.14).
The probable internal error on W  is estimated to be of the order of 0.3 mÅ.
is estimated to be of the order of 0.3 mÅ.
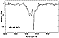 Fig.15
Another illustrative observation is given in Fig.15. It concerns the
absorption profile of the Ca II K line at 3933 Å, of the star
BD+46° 3471 (V = 10.2, B9.5 Ve). The spectrum has been obtained
by J. Czarny (Paris-Meudon Observatory) on September 12, 1989. The air
mass was around 1.02 and the integration time 3 h 25 min. A resolving
power of 12 300 (reciprocal linear dispersion of 8.2 Å/mm) was
provided by the grating N° 2. The signal-to-noise at the continuum
level is around 80. During the whole observation, the seeing was good
enough to collect a large part of the starlight within the circular
entrance hole of 3 arcsec. Although the sky was sometimes a little bit
foggy, the atmospheric absorption was certainly smaller than usual.
Fig.15
Another illustrative observation is given in Fig.15. It concerns the
absorption profile of the Ca II K line at 3933 Å, of the star
BD+46° 3471 (V = 10.2, B9.5 Ve). The spectrum has been obtained
by J. Czarny (Paris-Meudon Observatory) on September 12, 1989. The air
mass was around 1.02 and the integration time 3 h 25 min. A resolving
power of 12 300 (reciprocal linear dispersion of 8.2 Å/mm) was
provided by the grating N° 2. The signal-to-noise at the continuum
level is around 80. During the whole observation, the seeing was good
enough to collect a large part of the starlight within the circular
entrance hole of 3 arcsec. Although the sky was sometimes a little bit
foggy, the atmospheric absorption was certainly smaller than usual.
 Fig.16
Finally, Fig.16
shows a series of consecutive spectra of the Si III line profile of
the
Fig.16
Finally, Fig.16
shows a series of consecutive spectra of the Si III line profile of
the
 Cephei
variable star 12 Lac (<V> = 5.25 for a maximum amplitude of 0.11).
They have been obtained by P. Mathias (Katholieke Universiteit Leuven)
on September 4, 1989 with a resolving power of 15 000. The grating N°
2 providing a reciprocal linear dispersion of 8.1 Å/mm was used.
The signal-to-noise ratio at the continuum level is around 180 and the
typical elapsed time between two consecutive spectra is 6 min 24s. The
observations cover one pulsating period (P = 4 h 38 min).
Note that the depth of the
Si III
Cephei
variable star 12 Lac (<V> = 5.25 for a maximum amplitude of 0.11).
They have been obtained by P. Mathias (Katholieke Universiteit Leuven)
on September 4, 1989 with a resolving power of 15 000. The grating N°
2 providing a reciprocal linear dispersion of 8.1 Å/mm was used.
The signal-to-noise ratio at the continuum level is around 180 and the
typical elapsed time between two consecutive spectra is 6 min 24s. The
observations cover one pulsating period (P = 4 h 38 min).
Note that the depth of the
Si III 
 4553 line is only around 20% under the continuum level. This last example
illustrates well the ability of AURELIE for high time resolution observations.
4553 line is only around 20% under the continuum level. This last example
illustrates well the ability of AURELIE for high time resolution observations.
Conclusions
AURELIE is a simple, low cost and very flexible spectrometer. It can
be used
from a resolving power of 4 000 up to 110 000. The lack of interference
fringes
and persistence effects of the double linear array TH 7832 allows to
obtain very clean spectra. Spectral domains varying from 880 Å,
to 27 Å (depending on the dispersion) are spread over 2048 13
µm wide pixels. A high optical transmission (0.90), modified Bowen-Walraven
image-slicer is used to improved the resolution of the spectrometer.
The comparison of performances with the ESO-CES shows that a moderate-sized,
low cost instrument such as AURELIE can successfully compete with a
larger, more expensive instrument. This kind of approach is an important
point at a time when many groups are defining high-resolution spectrographs
for 8-10 m-class telescopes. Finally, the key factors of the "AURELIE
solution" are the use of an image slicer, of a cylindric lens and of
the linear detector format. Moreover, if a large size, high quantum
efficiency, low read-out noise CCD device would become available, we
must expect that the performance of AURELIE would significantly improve,
at least at low
signal-to-noise ratios.
acknowledgements. The authors are indebted to J.L. Coutures
of
Thomson-CSF and Thanh Nguyen Trong of the Laboratoire d'Astronomie Spatiale
of
Marseille for their assistance during the development and testing of
the
detector and to Drs. S. D'Odorico and H. Dekker for their critical reading
of
the paper. Finally one of the authors (DG) is indebted to B. Buzzoni,
B.
Delabre, D. Enard and G. Lund (ESO) for many informative conversations
at the
beginning of this projet and especially about the modified Bowen-Walraven
image-slicer developed at ESO.
Bibliography
Baranne A., Duchesne M.,
1976, Photo-Electronic Image Devices, Sixth symposium (1974),
Eds. B.L. Morgan et al, in Advances in Electronics and Electron Physics Vol. 40B,
Academic Press, London, page 641.
Coutures J.L., Boucharlat G.,
1988a, The Impact of Very High S/N Spectroscopy on Stellar Physics,
IAU Symp. N° 132, Eds. G. Cayrel de Strobel, M. Spite,
Kluwer Academic Publishers, Dordrecht, page 45.
Coutures J.L., Boucharlat G.,
1988b, Photo-Electronic Image Devices, Ninth symposium (1987),
Ed. B.L. Morgan, in Advances in Electronics and Electron Physics Vol.74,
Academic Press, London, page 173.
Coutures J.L., Boucharlat G.,
1987, Thomson-CSF internal report N° 3354.
Enard D.,
1982, Proceedings of SPIE 331,
Instrumentation in Astronomy IV, page 232.
Lemaitre G., Kohler D., Lacroix D., Meunier J.P., Vin A.,
1990, A&A 228, 546.
Lund G., Ferlet R.,
1984, The Messenger 36, 2.
Walraven Th., Walraven J.H.,
1972, Auxilary instrumentation for large telescopes, ESO/CERN conference,
Ed. S. Lausten and A. Reiz, june 1972,
ESO publication, page 175.
2.12.97
HTML: S.A.I. & R.G.
[ Présentation d'Aurélie |
Guide Pratique |
Page d'accueil OHP ]
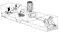 Fig.1b
The collimator and the camera are two spherical mirrors and the grating
is located at their common curvature center. The aperture of the collimator
and the camera are f/10 for a pupil diameter of 100 mm. 100% of the
residual spherical aberration produced by the whole optical system before
the cylindrical lens is in a circle of 19 µm in diameter.
Fig.1b
The collimator and the camera are two spherical mirrors and the grating
is located at their common curvature center. The aperture of the collimator
and the camera are f/10 for a pupil diameter of 100 mm. 100% of the
residual spherical aberration produced by the whole optical system before
the cylindrical lens is in a circle of 19 µm in diameter.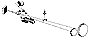 Fig.1a
The use of a modified Bowen-Walraven image-slicer (Walraven and Walraven
1972, Lund and Ferlet 1984), together with a long focal length (1 m)
camera and a detector having a large number (2048) of small size (13
µm) pixels, was found to be a good solution. Indeed, to obtain
the same resolving power with an entrance aperture of 3 arcsec and without
image-slicer, an unreasonable pupil diameter of 500 mm and an aperture
of camera of f/2 would be required. The general principle of the instrument
is classical (see Fig.1a, Fig.1b).
Fig.1a
The use of a modified Bowen-Walraven image-slicer (Walraven and Walraven
1972, Lund and Ferlet 1984), together with a long focal length (1 m)
camera and a detector having a large number (2048) of small size (13
µm) pixels, was found to be a good solution. Indeed, to obtain
the same resolving power with an entrance aperture of 3 arcsec and without
image-slicer, an unreasonable pupil diameter of 500 mm and an aperture
of camera of f/2 would be required. The general principle of the instrument
is classical (see Fig.1a, Fig.1b). Fig.2
Fig.2 Fig.3
Fig.3 Fig.4
Fig.4 Fig.5a
Fig.5a Fig.5b
Fig.5b Fig.6
Fig.6 Fig.7a
Fig.7a Fig.7b
Fig.7b Fig.8
Fig.8 Fig.9
Fig.9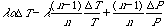 ,
,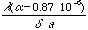 ,
, Fig.10
Fig.10 Fig.11
Fig.11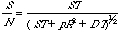 ,
, Fig.12
Fig.12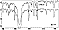 Fig.13
Fig.13 Fig.14
Fig.14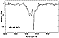 Fig.15
Fig.15 Fig.16
Fig.16